Формула Стокса

Для поверхневих інтегралів має місце формула, аналогічна формулі Гріна. Існують різні шляхи виведення цієї формули, обгрунтовані до найменших подробиць, але ними ж і обтяжені. Зупинимось на дещо полегшеному варіанті, зате на такому, який наглядно ілюструє суть усіх різновидів – зв'язок поверхневого інтегралу з подвійним, а останнього – через формулу Гріна – з криволінійним.

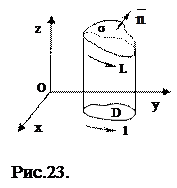
Розглянемо у просторі деяку поверхню s, обмежену лінією L. Проекцією цієї поверхні на площину XOY буде область D, обмежена замкненою лінією l. Нехай у просторі задано векторне поле 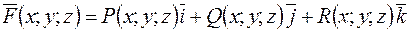. Якщо покласти z=0 і R(x;y;z)º0, матимемо плоске векторне поле, яке в області D приймає значення .

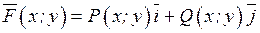Обчислимо ротор цього векторного поля: .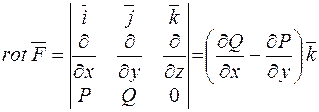

Тоді потік цього ротора через область D буде: .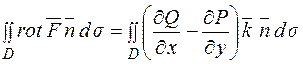

Оскільки нормаль 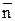до області D співпадає з 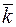, тобто 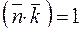і згадуючи формулу Гріна, маємо: .

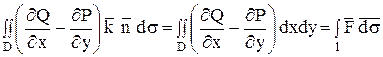Остаточно: .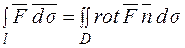

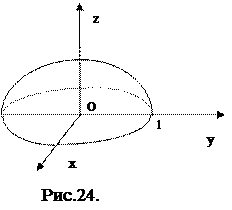У просторі для замкненої поверхні s, обмеженої лінією l, формула залишиться в тому ж вигляді 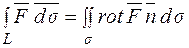, при цьому напрямок обходу контуру L погоджується з обраною стороною поверхні таким чином: якщо дивитися з кінця вектора нормалі до поверхні, то цей обхід здійснюється проти ходу годинникової стрілки. Висновок: циркуляція векторного поля 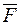по замкненій лінії L, яка обмежує поверхню s, дорівнює потоку ротора цього векторного поля через цю поверхню.

Приклад. Обчислити потік ротора векторного поля 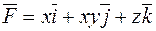через поверхню s: x²+y²+z²=1, z ³ 0.

Розв'язання. Поверхня s являє собою півсферу, радіус якої дорівнює 1, а L відповідно – коло в площині XOY.

Отже: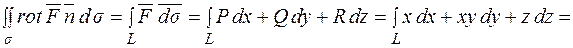

Далі, врахуємо, що L лежить в площині XOY, значить z=0, і перейдемо до параметричних координат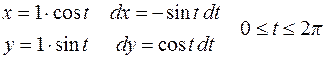

.

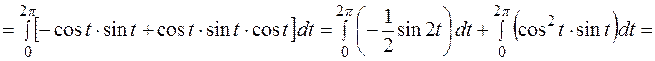
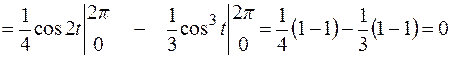Принагідно зауважити, що, коли векторне поле потенціальне, 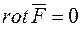. За формулою Стокса якщ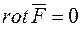о , то 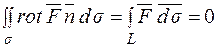це означає, що векторне поле потенціальне. Інакше – потенціальне векторне поле є безвихорним.

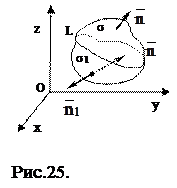Із формули Стокса виходить, що потік вихора векторного поля 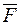не залежить від виду поверхні s, яка "натягнута" на контур L. Якщо через цей контур провести дві поверхні s₁ та s₂, то . За правилами орієнтації поверхні s₂ очевидно 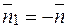, а, отже,

.

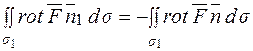З іншого боку, поверхні s₁ та s₂ обмежують деякий об'єм V, для поверхні якого одержуємо рівність:

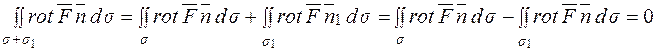Отже, потік вихора векторного поля 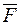через замкнену поверхню дорівнює нулю.

Якщо в деякій частині поля 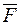(або в усьому полі) 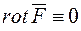, то 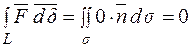де L ‑ довільний контур, який лежить цілком у зазначеній частині поля.