Ротор векторного поля

За означенням ротор (або вихор) векторного поля

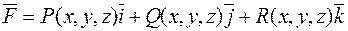
має вигляд

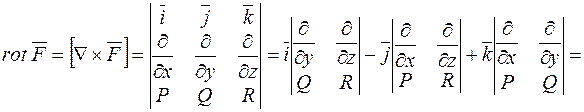
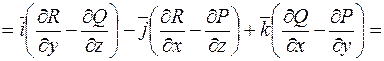
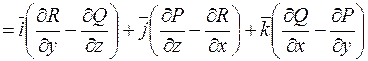
Підсумуємо властивості ротора:

1. Ротор сталого вектора дорівнює нулю rot a=0 a=const;

2. ;

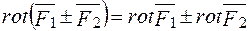3. ;

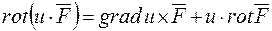4. ;

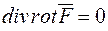5. .

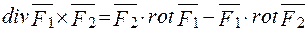Нехай тепер задане поле – потенціальне, а u=u(x,y,z) ‑ його потенціал. Тоді .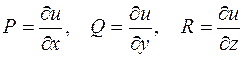

Обчислимо ротор потенціального поля:

.

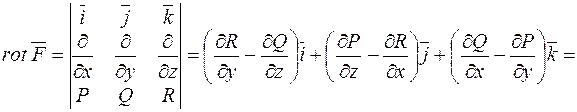
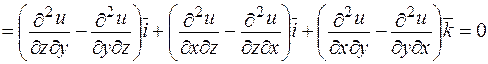Отже, 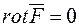, якщо поле ‑ потенціальне.

Зворотне твердження також вірне.

Означення. Векторне поле будемо називати безвихорним, якщо його ротор дорівнює нулю.

Тож всяке потенціальне поле є безвихорним.

Зокрема, рівність rot grad u=0 свідчить про те, що поле градієнтів завжди потенціальне.

Висновок: щоб визначити, чи буде задане поле потенціальним, достатньо пересвідчитись, щоб його ротор дорівнював нулю.

Приклад: Пересвідчитись, що векторне поле 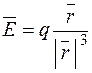потенціальне, і обчислити його потенціал (q=const).

.

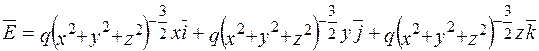Позначимо: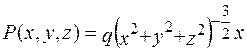

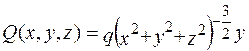
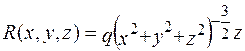
Тоді, наприклад,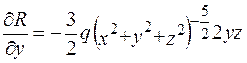

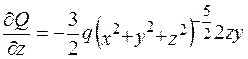
і вираз у дужках .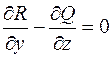

Аналогічно можна показати, що два інші вирази в дужках також дорівнюють нулю, а, отже, 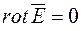, значить, 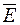‑ потенціальне.

Обчислимо його потенціал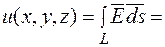

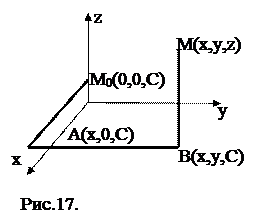
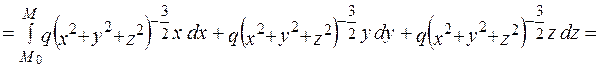
виберемо початкову точку M₀(0;0;C) (C=const), і шлях інтегрування:

M₀A: y=0, z=C, dy=0, dz=0

AB: x=x=const, z=C, dx=0,

dz=0

BM: x=x=const, y=y=const,

dx=0, dy=0

тоді: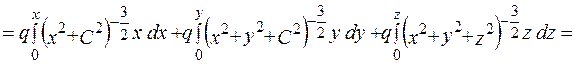

.

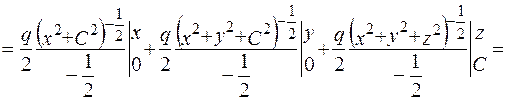
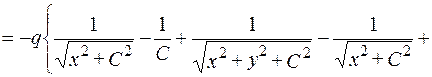
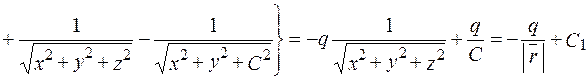Отже, скалярний потенціал поля 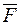в точці M(x;y;z) дорівнює циркуляції вектора 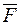уздовж довільної кривої, що з'єднує точку M з точкою M₀, в якій потенціал поля прийнятий рівним нулю.

Якщо потенціальне поле 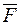‑ силове, то потенціал цього поля у точці M(x;y;z) чисельно дорівнює роботі сили уздовж довільної кривої, яка з'єднує точку M з точкою нульового потенціалу M₀.