Розбіжність поля. Формула Остроградського

Нехай маємо векторне поле 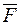. Візьмемо в ньому довільну точку P і розмістимо її всередині замкнутої поверхні s, яка обмежує об'єм Dv.

Знайдемо 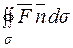‑ потік вектора 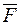через замкнену поверхню s (в напрямку зовнішньої нормалі).

Обчислимо величину .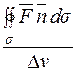

Припустимо, що існує границя цієї величини за умови, якщо поверхня s стягується в точку P. Ця границя зветься розбіжністю або дивергенцією векторного поля 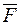і позначається:

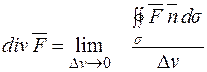
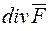є скалярною величиною. Якщо в точці P 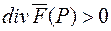, то для досить малого Dv 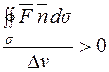, і оскільки Dv>0, то 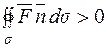, що за фізичним змістом потоку векторного поля означає, що в точці Р маємо джерело поля. Якщо 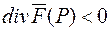, тоді в точці P маємо стік поля. У точках, де 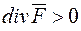векторні лінії починаються, а в точках, де 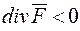, вони закінчуються.

Векторне поле, в кожній точці якого 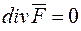, називається соленоїдальним (або трубчатим). У такому полі немає ані джерел, ані стоків.

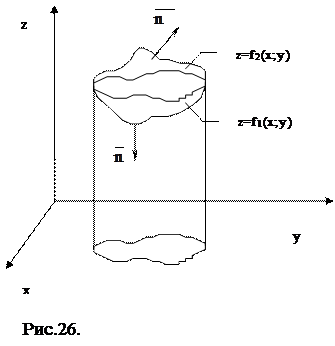Розглянемо у просторі тіло V, обмежене замкненою поверхнею s (Рис.26). Проекцію тіла на площину XOY позначимо через D. Лінія на поверхні тіла, яка проектується в границю області D, поділяє поверхню s на дві частини s₊ та s_‑, які описуються функціями відповідно z=f₂(x;y) та z=f₁(x;y). Окрім того, будемо відрізняти зовнішню сторону поверхні та внутрішню в залежності від направленості нормалі до поверхні. Нехай тепер у цьому просторі задано векторне поле

.

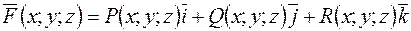Обчислимо потрійний інтеграл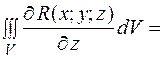

.

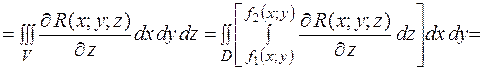
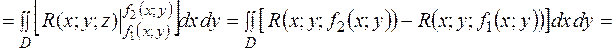
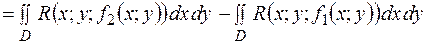Перетворимо одержані подвійні інтеграли в поверхневі. Для цього розглянемо поверхневий інтеграл

,

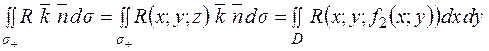враховуючи, що .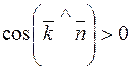

Аналогічно:

,

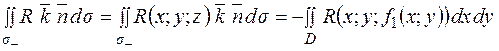враховуючи, що в цьому випадку 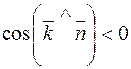склавши одержані два інтеграли, маємо:

.

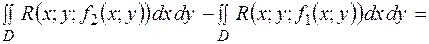
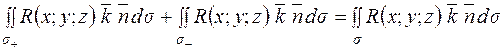Таким чином .

Аналогічно можна обчислити:

;

.

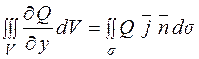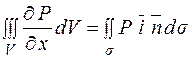Склавши ці три рівності, маємо:

.

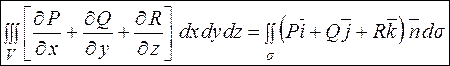Ця рівність і є формулою Остроградського.

Використаємо формулу в наступній теоремі:

Теорема. Дивергенція векторного поля 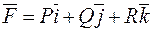виражається формулою 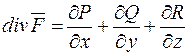, де значення частинних похідних беруться в точці M.

Доведення. За формулою Остроградського потік векторного поля можна записати у вигляді

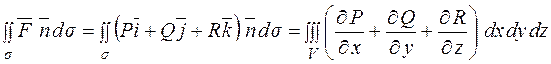
Потрійний інтеграл за теоремою про середнє значення дорівнює добутку об'єму V на значення підінтегральної функції в деякій точці M₁ області V, тобто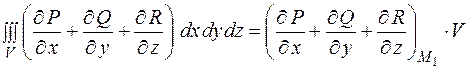

Якщо об'єм V стягується в точку M, то точка M₁ також прямує до точки M, і ми маємо

,

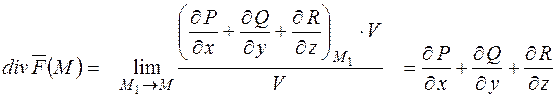що і треба було довести.

Користуючись одержаним виразом для дивергенції, тепер і формулу Остроградського можна записати у вигляді: 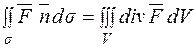, тобто потік векторного поля з середини замкнутої поверхні дорівнює потрійному інтегралу за об'ємом, обмеженим цією поверхнею від дивергенції поля.

Розглянемо соленоїдальне (або трубчате) поле саме таке, для якого .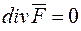

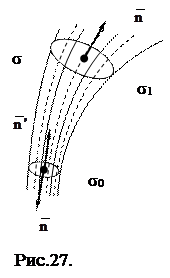Візьмемо в цьому полі яку-небудь площинку s₀ і проведемо через кожну точку її границі векторні лінії. Ці лінії обмежують частину простору, так звану векторну трубку. Рідина рухається в цій трубці, не перетинаючи її стінок. Розглянемо частину цієї трубки, обмеженою вже згадуваною площинкою s₀ і s₁ деяким перерізом (Рис.27).

Оскільки умовою 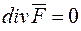, то потік векторного поля через будь-яку замкнену поверхню дорівнює нулю, отже

,

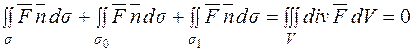де s ‑ бічна поверхня трубки, а 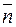‑ зовнішня нормаль.

Оскільки на бічній поверхні трубки нормаль 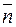перпендикулярна до векторної лінії поля, то .

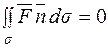Тоді виходить, що .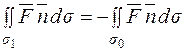

Якщо змінити напрямок нормалі на площинці s₀, тобто взяти внутрішню нормаль 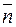, то одержимо: .

Це означає, що потік вектора в напрямку векторних ліній через кожний переріз векторної трубки один і той же, тобто в полі без джерел через кожний переріз векторної трубки протікає одна й та ж кількість рідини.

Відповідно до формули 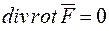поле ротора довільного векторного поля – трубчате. Справедливо й зворотне твердження – кожне трубчате поле є полем ротора деякого векторного поля, тобто якщо 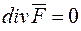, то існує таке векторне поле 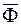, що .

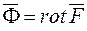Вектор 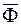називають вектором-потенціалом даного поля.