Вихревой характер магнитного поля. Закон полного тока

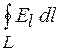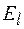При рассмотрении электростатического поля использовалось понятие циркуляции вектора напряженности , где – проекция вектора 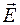на направление элемента 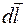замкнутого контура L. В магнитном поле рассматривают циркуляцию вектора магнитной индукции, т. е. выражение .

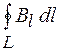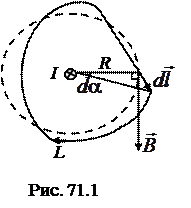Рассчитаем циркуляцию вектора магнитного поля, созданного бесконечно длинным прямолинейным проводником с током (рис. 71.1). В качестве замкнутого контура L возьмем произвольный контур, лежащий в плоскости, перпендикулярной проводнику. Ток направлен за чертеж.

В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку. Входящее в выражение циркуляции произведение 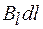можно преобразовать следующим образом:

,

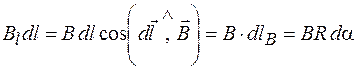где 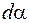– угол поворота радиальной прямой при перемещении вдоль контура на расстоянии .

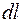Используем полученное выражение и формулу (68.8) для индукции поля прямого тока при вычислении циркуляции вектора :

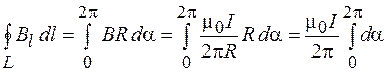. (71.1)

При обходе по контуру, охватывающему проводник с током, радиальная прямая описывает угол 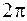, поэтому 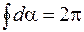. В результате формула (71.1) принимает вид

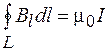. (71.2)

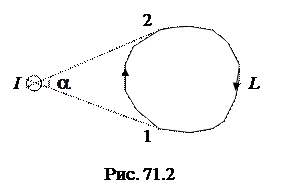Если контур не охватывает проводник с током (рис. 71.2), то радиальная прямая сначала поворачивает на угол 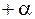(участок 1–2), а потом на угол 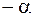(участок 2–1). В результате 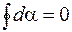и 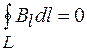, что совпадает с выражением (71.2), если под 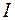подразумевать силу тока, охватываемого контуром (в данном случае I = 0).

Если контур охватывает несколько токов, то в соответствии с принципом суперпозиции

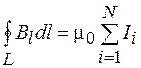. (71.3)

Циркуляция вектора магнитной индукции равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых контуром.

Выражение (71.3) называют законом полного тока или теоремой о циркуляции вектора . В этом выражении ток считают положительным, если он составляет с направлением обхода контура L правовинтовую систему, и наоборот.

Формула (71.3) справедлива для любых токов и контуров, охватывающих эти токи.

Учитывая соотношение (65.6), закон полного тока для вектора 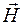из формулы (71.3) получаем в форме

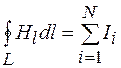. (71.4)

Как видно из соотношения (71.3), циркуляция вектора может быть не равна нулю, что значительно отличает магнитное поле от электростатического. Поле, циркуляция вектора которого не равна тождественно нулю, называют вихревым полем. Поэтому магнитное поле является вихревым. Вихревой характер магнитного поля означает, что линии вектора магнитной индукции замкнуты, в чем мы убедились раньше на конкретных примерах магнитных полей. Замкнутость линий вектора магнитной индукции означает, что поток вектора через любую замкнутую поверхность равен нулю, т. е.

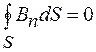. (71.5)

Равенство нулю циркуляции вектора 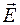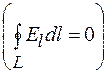и неравенство нулю потока этого вектора через замкнутую поверхность в случае электростатического поля говорит о том, что линии напряженности этого поля не замкнуты, и поле не вихревое, а потенциальное (§ 26).

Закон полного тока, подобно теореме Гаусса для электрического поля, позволяет рассчитывать магнитные поля, обладающие различными типами симметрии, без использования закона Био–Савара.

Рассмотрим два примера применения закона полного тока.

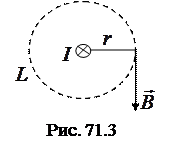Магнитное поле прямого тока. Пусть прямой ток I направлен перпендикулярно плоскости чертежа от нас (рис. 71.3). Выберем воображаемый контур в форме окружности радиуса 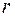. Контур совпадает с одной из линий индукции. В результате в каждой точке контура вектор направлен по касательной и одинаков по модулю, а циркуляция вектора магнитной индукции равна

.

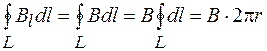В соответствии с выражением (71.3) получим:

,

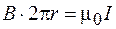откуда

. (71.6)

Таким образом, используя закон полного тока, мы достаточно просто получим формулу индукции магнитного поля прямого тока.

Другим примером применения закона полного тока служит расчет поля соленоида.