Магнитное поле кругового тока

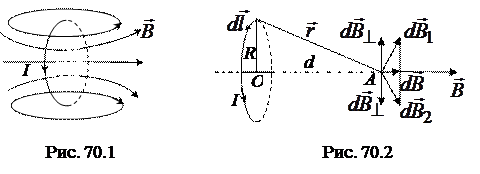Линии магнитной индукции поля кругового тока имеют вид, показанный на рисунке 70.1. Направление вектора 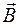с направлением тока I связано правилом правого винта: направление вращения винта совпадает с направлением тока, поступательное движение винта укажет направление вектора 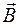. Рассчитаем индукцию 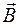в точках, лежащих на оси кругового тока (рис. 70.2). Разделим мысленно контур на элементарные участки 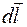. Выделим участок в верхней части контура. Элемент тока 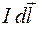создает в точке А, отстоящей от плоскости тока на расстоянии d, элементарную индукцию 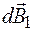, численное значение которой определяется законом Био–Савара. Так как 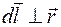, то из формулы (68.2) находим:

. (70.1)

Элемент тока, выделенный в нижней части контура симметрично первому, создает в точке А индукцию 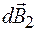. Разложим векторы 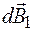и 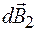на составляющие 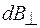и 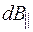. Составляющие 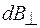компенсируют друг друга, а составляющие 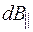оказываются параллельными. Множество векторов 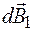, 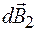и т. д. полей, создаваемых одинаковыми элементами проводника 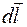, образуют в точке А конический веер, ось которого совпадает с осью кругового тока. Это позволяет сделать вывод, что вектор 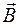результирующего поля в точке А направлен вдоль оси. Поэтому можно суммировать проекции 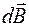на ось кругового тока: 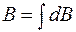. Из рисунка 70.2 находим:

.

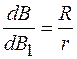Отсюда

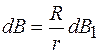. (70.2)

Тогда из формул (70.1) и (70.2) получаем:

.

Для индукции поля кругового тока имеем:

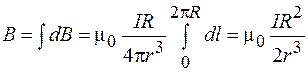. (70.3)

Из рисунка (70.2) видно, что 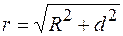, поэтому

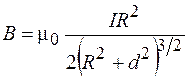. (70.4)

Для точки, находящейся в центре кругового тока, 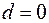и для нее из формулы (70.4) находим:

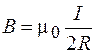. (70.5)

Умножив числитель и знаменатель выражения (70.3) на число 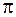, находим:

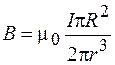. (70.6)

Величина

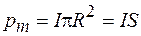(70.7)

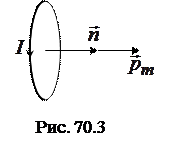называется магнитным моментом контура. Вектор 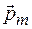перпендикулярен плоскости контура и связан с направлением тока в контуре правилом правого винта (буравчика) (рис. 70.3). Направление вектора 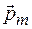совпадает с направлением положительной нормали 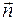к контуру. Единица магнитного момента – ампер-метр в квадрате ( 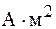). Если контур составлен из N витков, то его магнитный момент 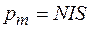. Из формул (70.8) и (70.9) получаем:

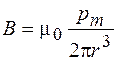. (70.8)

Выражение (70.8) аналогично формуле (26.5) для расчета напряженности электрического поля диполя. Но тогда следует ожидать аналогию поведения кругового тока в магнитном поле с поведением диполя в электрическом поле. Это означает, что магнитное поле должно определенным образом ориентировать круговой ток, создавая некоторый вращающий момент.

Полученные в этом параграфе результаты можно использовать для расчета магнитного поля катушки с током. Выделим малый участок катушки длиной 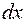, который ввиду малости можно рассматривать как круговой контур, сила тока в котором равна 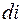(рис. 70.4). Применяя формулу (70.4), вычислим индукцию 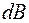поля, созданного на оси в точке А выбранным элементом катушки:

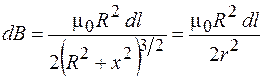, (70.9)

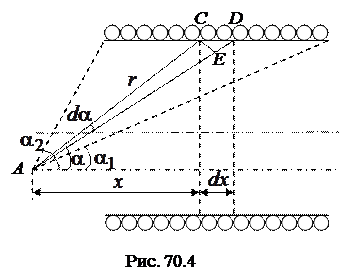
где R – радиус витка катушки.

Сила тока 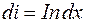, где 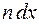– число витков соленоида на участке 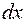; I – сила тока в одном витке. Величину 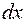можно выразить через r, 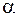, 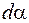с применением тригонометрических формул:

.

Тогда 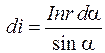. Кроме того, .

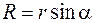Используя полученные результаты, формулу (70.9) приведем к виду, удобному для интегрирования:

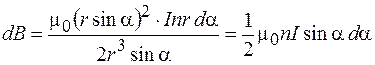. (70.10)

Векторы 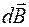полей, созданных различными участками 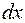катушки, направлены одинаково и совпадают с ее осью. Поэтому для определения модуля вектора индукции результирующего поля проинтегрируем выражение (70.10) по переменной 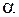в пределах от 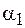до :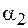

.

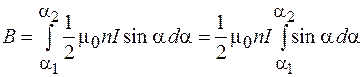Выполнив интегрирование, получим:

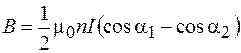, (70.11)

где 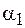и 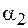– углы, под которыми из точки наблюдения видны радиусы оснований катушки.

Если катушка длинная, то для точки А,находящейся в ее средней части, можно принять , 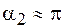и тогда, согласно формуле (70.11), индукция равна

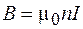. (70.12)

Согласно формуле (70.12) индукция магнитного поля длинного соленоида пропорциональна числу ампер-витков 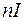, приходящихся на единицу длины катушки. В точке А, находящейся в центре одного из оснований такой катушки,

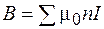. (70.13)

Если катушка с сердечником, то в выражении для магнитной индукции появится множитель, равный относительной магнитной проницаемости 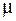вещества сердечника.

Для получения сильных полей используют магнитные материалы с большой магнитной проницаемостью. К ним относятся ферромагнетики (железо, никель, кобальт), их сплавы и соединения.