Магнитное поле тороида

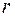Тороид представляет собой систему одинаковых круговых токов, плотно навитых на каркас в виде тора (рис. 73.1). Линии магнитной индукции в данном случае имеют вид окружностей, центры которых находятся на оси тороида. Рассчитаем циркуляцию вектора по контуру радиуса , совпадающему с одной из этих окружностей. Во всех точках этого контура значение магнитной индукции одинаково и вектор направлен по касательной. Поэтому 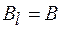и тогда

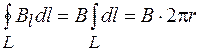. (73.1)

Воспользуемся законом полного тока (71.3) и учтем, что токи, охватываемые контуром, одинаково направлены, т. е. 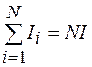, где N – число витков тороида. Тогда из формулы (73.1) получаем:

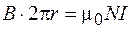. (73.2)

Отсюда находим:

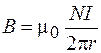. (73.3)

Поле тороида полностью сосредоточено внутри него, но оно не является однородным. В разных сечениях тороида направление вектора будет разным. Кроме того, в пределах одного сечения модуль вектора в разных точках будет разным. Около внутренней поверхности (в точке А) индукция имеет максимальное значение, вблизи внешней (в точке С) – минимальное.

Число витков тороида можно выразить через его длину (по средней линии) и плотность намотки: 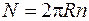. Тогда формула (73.3) приводится к виду

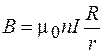, (73.4)

где R – радиус средней линии.

Если диаметр витка много меньше радиуса средней линии, то для всех точек в тороиде 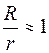. В этом случае формула (73.4) совпадает с выражением (72.7) для бесконечного соленоида: 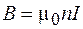. Это означает, что модуль вектора во всех точках внутри такого тороида имеет одинаковое значение, а в пределах данного поперечного сечения поле можно считать однородным.

Если контур проходит вне тороида, то токов он не охватывает и как следует из выражения (73.3) . А это означает, что магнитное поле вне тороида отсутствует.