Оператор Гамільтона у векторному полі
Нехай задано векторне поле
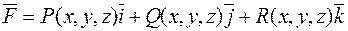 .
.
Застосуємо оператор "набла" до цього векторного поля за правилами множення векторів. Оскільки добуток двох векторів може бути або скалярним, або векторним, то розглянемо спочатку скалярний добуток:
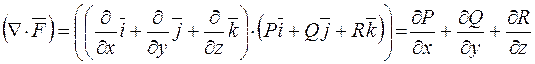 .
.
Такий добуток має назву дивергенція і позначається так 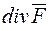 .
.
Отже, 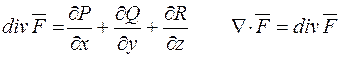 .
.
Наприклад, для вектора
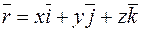
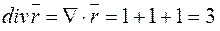 .
.
Розглянемо тепер векторний добуток, що означає соленоїдальність поля
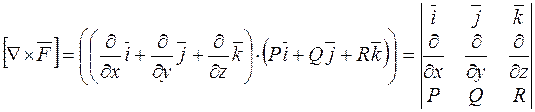 .
.
Такий добуток має назву ротор, і позначається:
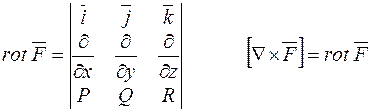 .
.
Приклад. Знайти ротор векторного поля
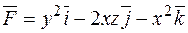 .
.
Розв'язання. 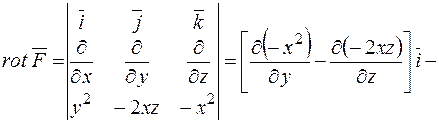
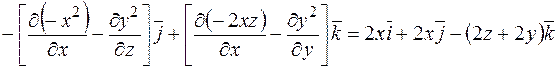 .
.
Застосування оператора Гамільтона до суми скалярних полів здійснюється за правилами чисельного добутку: 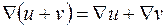 .
.
Застосування оператора Гамільтона до суми векторних полів здійснюється за правилами скалярного добутку: 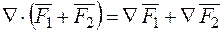 .
.
або за правилами векторного добутку:
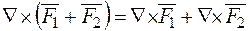 .
.
Дата добавления: 2015-07-22; просмотров: 697;
