Векторне поле
Нехай в деякій області простору задано векторне поле
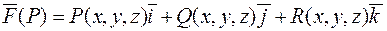 ,
,
де 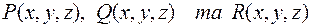 ‑ скалярні функції.
‑ скалярні функції.
Означення. Векторною лінією поля 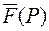 зветься лінія, дотична до якої в кожній її точці співпаде з вектором
зветься лінія, дотична до якої в кожній її точці співпаде з вектором 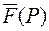 , що визначає поле в цій точці.
, що визначає поле в цій точці.
Прикладами векторних ліній поля в електротехніці є лінії вектора напруги магнітного поля 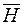 чи лінії вектора напруги електричного поля
чи лінії вектора напруги електричного поля 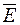 . Лінії вектора
. Лінії вектора 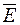 називають силовими лініями внаслідок того, що напруга електричного поля чисельно дорівнює силі, яка діє в даній точці поля на одиничний додатній заряд. Напрямки вектора цієї сили та вектора
називають силовими лініями внаслідок того, що напруга електричного поля чисельно дорівнює силі, яка діє в даній точці поля на одиничний додатній заряд. Напрямки вектора цієї сили та вектора 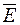 завжди співпадають.
завжди співпадають.
Виведемо диференціальне рівняння векторних ліній.
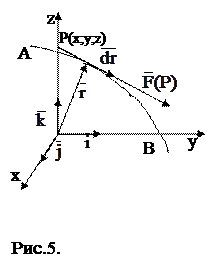 Нехай (рис.5) AB ‑ векторна лінія,
Нехай (рис.5) AB ‑ векторна лінія,  ‑ радіус-вектор точки P(x;y;z). Тоді
‑ радіус-вектор точки P(x;y;z). Тоді 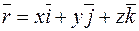 .
.
Обчислимо 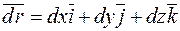 .
.
З диференціального числення відомо, що вектор 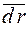 направлений по дотичній до AB в точці P. Отже,
направлений по дотичній до AB в точці P. Отже, 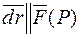 , але тоді з умови паралельності векторів
, але тоді з умови паралельності векторів 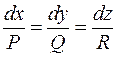 .
.
Це і є диференціальне рівняння векторних ліній. Якщо векторне поле за природою є поле сили, то і його векторні лінії будуть силовими.
Якщо векторне поле задано на площині, то таке поле будемо називати плоским: 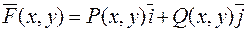 .
.
Приклад. Постійний електричний струм I тече по нескінченно довгому провіднику, співпадаючому з віссю OZ в напрямку знизу вгору. Вектор напруги магнітного поля 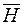 , створюваного цим струмом, в довільній точці P(x;y;z) дорівнює
, створюваного цим струмом, в довільній точці P(x;y;z) дорівнює
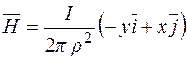 ,
,
де 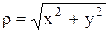 ‑ відстань від P(x;y;z) до осі OZ. Знайти векторні лінії магнітного поля
‑ відстань від P(x;y;z) до осі OZ. Знайти векторні лінії магнітного поля 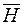 .
.
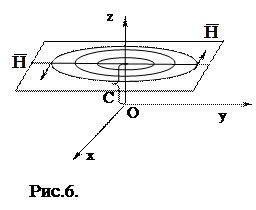 Розв'язання. Запишемо векторне поле у вигляді
Розв'язання. Запишемо векторне поле у вигляді 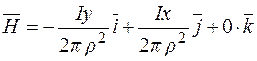 , тобто
, тобто 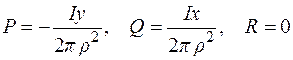 .
.
Диференціальне рівняння векторних ліній після очевидних скорочень набуде вигляду: 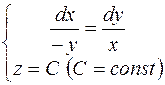 або
або 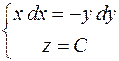
Після інтегрування: 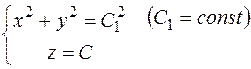
Дата добавления: 2015-07-22; просмотров: 775;
