Градієнт
Нехай задано скалярне поле u = u(x;y;z), причому функція u має частинні похідні 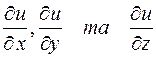 .
.
Вектор  зветься градієнтом скалярного поля u і позначається:
зветься градієнтом скалярного поля u і позначається:
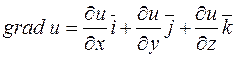
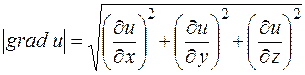 .
.
Розглянемо зв'язок між градієнтом та похідною за напрямком.
Теорема. Нехай задано скалярне поле u=u(x;y;z) і в ньому визначено скалярне поле градієнтів 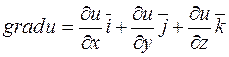 .
.
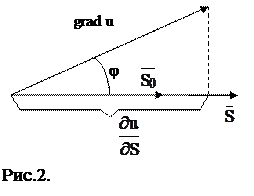 Похідна
Похідна 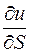 за напрямком деякого вектора
за напрямком деякого вектора 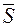 дорівнює проекції вектора grad u на вектор
дорівнює проекції вектора grad u на вектор 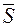 .
.
Доведення. Розглянемо одиничний вектор 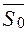 , відповідний вектору
, відповідний вектору 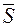 :
: 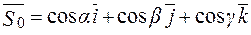 .
.
Обчислимо скалярний добуток
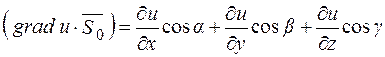 .
.
Вираз у правій частині є не що інше, як похідна від функції u=u(x;y;z) за напрямком 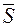 :
: 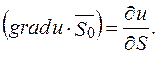
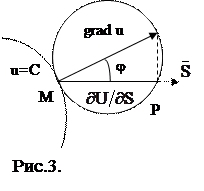 Якщо позначити кут між векторами grad u та
Якщо позначити кут між векторами grad u та 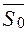 через j (рис.2.), то можна записати
через j (рис.2.), то можна записати 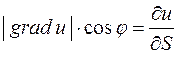 або
або 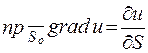 .
.
З доведеної теореми легко з'ясовується зв'язок між градієнтом та похідною в даній точці за напрямком.
У точці M(x;y;z) будуємо вектор gradu (рис.3.). Далі будуємо сферу, для якої gradu є діаметром. З точки M проводимо вектор 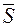 . Позначимо точку перетину його з поверхнею сфери через P. Тоді, очевидно,
. Позначимо точку перетину його з поверхнею сфери через P. Тоді, очевидно, 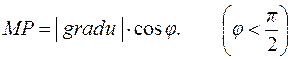 , тобто
, тобто 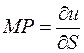 .
.
З'ясуємо деякі властивості градієнта.
1. Похідна в заданій точці за напрямком вектора 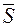 має найбільше значення, якщо напрямок вектора
має найбільше значення, якщо напрямок вектора 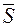 співпадає з напрямком градієнта; це найбільше значення похідної дорівнює
співпадає з напрямком градієнта; це найбільше значення похідної дорівнює 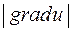 .
.
2. Похідна за напрямком вектора, перпендикулярного до вектора gradu, дорівнює нулю.
3. Нарешті, якщо функція u = u(x;y) є функцією двох змінних, то вектор 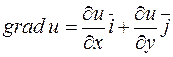 лежить у площині Оху.
лежить у площині Оху.
Доведемо, що gradu направлений перпендикулярно до лінії рівня u(x;y)=C, яка лежить в площині Оху і проходить через відповідну точку. Дійсно, кутовий коефіцієнт k1 дотичної до лінії рівня u(x;y)=C буде рівнятися  . Кутовий коефіцієнт k2 градієнта дорівнює
. Кутовий коефіцієнт k2 градієнта дорівнює  . Тоді k1* k2= -1. Це і доводить справедливість твердження.
. Тоді k1* k2= -1. Це і доводить справедливість твердження.
Приклад. Задана функція u=x2+y2+z2. Визначити градієнт в точці M(1;1;1).
Розв'язання: У довільній точці 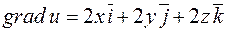 .
.
В точці M 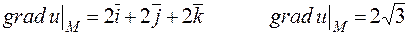 .
.
Дата добавления: 2015-07-22; просмотров: 1537;
