Похідна за напрямком
 Нехай задано скалярне поле u=u(P). Візьмемо у просторі точку P(x;y;z). Проведемо з точки Р вектор
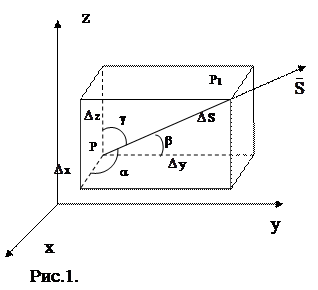
Нехай задано скалярне поле u=u(P). Візьмемо у просторі точку P(x;y;z). Проведемо з точки Р вектор 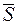 , який має направляючі косинуси cos a, cos b, cos g (рис.1.). На векторі
, який має направляючі косинуси cos a, cos b, cos g (рис.1.). На векторі 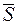 на відстані
на відстані 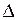 S від його початку розглянемо точку Р1 (x+
S від його початку розглянемо точку Р1 (x+ 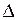 x; y+
x; y+ 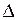 y;z+
y;z+ 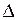 z). Таким чином
z). Таким чином 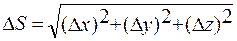 . Будемо вважати, що u=u(x;y;z) неперервна і має неперервні похідні.
. Будемо вважати, що u=u(x;y;z) неперервна і має неперервні похідні.
Повний приріст функції можна записати у вигляді
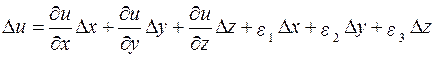 ,
,
де 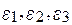 наближаються до нуля, якщо
наближаються до нуля, якщо 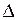 S®0.
S®0.
Поділимо рівність на 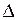 S:
S:
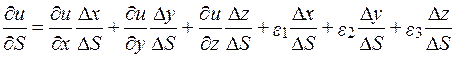 .
.
Враховуючи, що 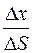 = cos a,
= cos a, 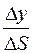 = cos b,
= cos b, 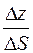 = cos g, цю рівність перепишемо так:
= cos g, цю рівність перепишемо так:
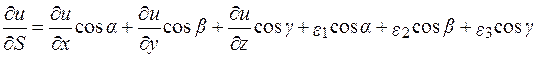 .
.
Границя відношення  при
при 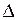 S®0 зветься похідною від функції u=u(x;y;z) в точці Р(x;y;z) за напрямком вектора
S®0 зветься похідною від функції u=u(x;y;z) в точці Р(x;y;z) за напрямком вектора  і позначається:
і позначається: 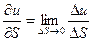 .
.
Таким чином 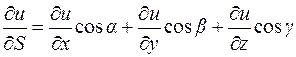 .
.
У випадку плоского поля u=u(x;y)
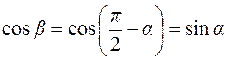 ;
; 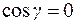 маємо:
маємо:
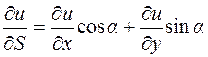 ,
,
де a ¾ кут, утворений напрямком  з віссю Ох.
з віссю Ох.
Приклад. Задано функцію u=x2+y2+z2. Знайти похідну 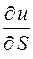 в точці P(1;1;1) в напрямку вектора
в точці P(1;1;1) в напрямку вектора 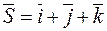 .
.
Розв'язання: Обчислюємо направляючі косинуси
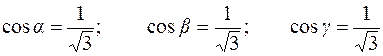 .
.
Далі 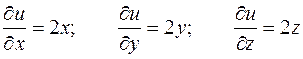
в точці P(1;1;1):  .
.
Отже, 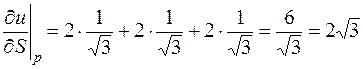 .
.
Дата добавления: 2015-07-22; просмотров: 643;
