Тема. Похідна складної функції
План
- Похідна складної функції.
1. Нехай потрібно обчислити за даним значенням х відповідне значення z функції h, заданою формулою
z = h(х)= 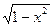 .
.
Для цього треба спочатку обчислити за даним х значення
у =f(х)= 1-х2,
а потім вже за цим уобчислити
z = g(у)= 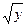
Отже, функція f ставить у відповідність числу х число у, а функція g - числу у число z. Говорять, що h є складна функція, складена з функцій g і f, і пишуть:
h(х) = g (f(х)).
Щоб обчислити значення складної функції h(х) = g (f(х)) у довільній точці х, спочатку обчислюють значення у «внутрішньої» функції f у цій точці, а потім g (у).
Яка область визначення складної функції g (f(х))? Це - множина всіх тих х з області визначення функції f, для яких f (х) входить в область визначення функції g.
У розглянутому прикладі областю визначення функції f є вся числова пряма. Значення h(х) визначене, якщо значення f (х) належить області визначення функції g(у) = 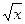 . Тому потрібно, щоб виконувалася нерівність в
. Тому потрібно, щоб виконувалася нерівність в 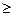 0, тобто 1 - х2
0, тобто 1 - х2 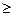 0, і, виходить, область визначення функції g (f (х)) - це відрізок [-1; 1].
0, і, виходить, область визначення функції g (f (х)) - це відрізок [-1; 1].
- Формула похідної складної функції.
У попередніх пунктах ви навчилися знаходити похідні раціональних функцій, зокрема многочленів. Однак задача обчислення похідної функції f(х) = (2х+3)100, хоча й зводиться до знаходження похідної многочлена, вимагає дуже великого об'єму роботи: треба представити (2х+3) у вигляді многочлена та продиференціювати 101доданок отриманої суми. Можна помітно спростити рішення цієї та інших задач.
Якщо функція f має похідну в точці х0, а функція g має похідну в точці у0 = f(х0), то складна функція h(х) = g (f(х)) також має похідну в точці хо, причому
h′(хо) = g′ (f(хо)) f′(хо).
Приклад 1. Знайдемо похідну функціїh(х) = (2х+3)100.
Функцію h можна представити у вигляді складної функції h(х) = g (f(х)), де g(у) = у100, у = f(х) = 2х+3.
Тому що f′(х) = 2 і g′ (у) = 100у99, маємо
h′(х) = 2* 100у99 = 200(2х+3)99.
| Таблиця похідних | ||
| Похідні елементарних функцій | Похідні складних функцій | |
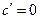
| ||
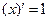 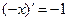
| ||
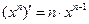
| 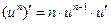
| |
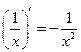 , х , х 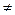 0 0
| 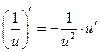 , х , х 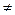 0 0
| |
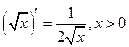
| 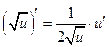
| |
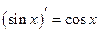
| 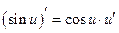
| |
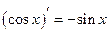
| 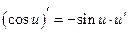
| |
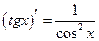
| 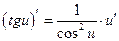
| |
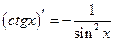
| 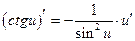
| |
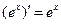
| 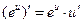
| |
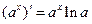 , a > 0, a - стала , a > 0, a - стала
| 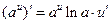
| |
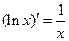 , , 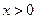
| 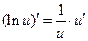
| |
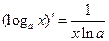 , , 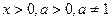 ,
a - стала ,
a - стала
| 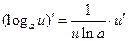
| |
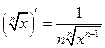 на ОДЗ правої частини формули
на ОДЗ правої частини формули
|
Вправи
- Задайте формулами елементарні функції f(x) і u(x), з яких складається складна функція
1) у = 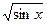 ;
;
2) у = (2х + х2)5;
3) у = 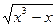 ;
;
4) у = соs(2х - 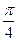 ).
).
- Знайдіть похідну функції f(x):
1) f(x) = (х2 + х)3;
2) f(x) = (2х - 1)-5;
3) f(x) = (х - 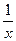 )4;
)4;
4) f(x) = 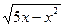 ;
;
5) f(x) = 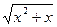 ;
;
6) у = 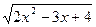 ;
;
7) у = (х2 - 2х)3;
8) s = (t2 – t + 1)4;
9) f(u) = 5(3u2 + 4 – u)4;
10) s = 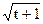 ;
;
11) у = 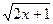 ;
;
12) f(x) = 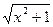 ;
;
13) f(x) = 2 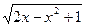 ;
;
14) у = 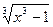 ;
;
15) у = 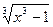 ;
;
16) f(t) = t2 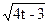 ;
;
17) f(t) = (t - 1) 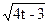 ;
;
18) f(t) = (t + 1)2 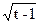 ;
;
19) f(x) = 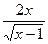 .
.
Дата добавления: 2015-08-26; просмотров: 2727;
