Тема. Приріст аргументу і приріст функцій. Задачі, які приводять до поняття похідної. Означення похідної, механічний та геометричний зміст
План
- Приріст аргументу і приріст функцій.
- Задачі, які приводять до поняття похідної.
- Означення похідної.
- Геометричний зміст похідної.
- Механічний зміст похідної.
- Приріст аргументу і приріст функції
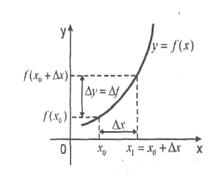
| Якщо змінна величина х змінила своє значення від х0 до х1, то різниця між її новим значенням і початковим називається приростом аргументу і позначається символом ∆х (читається: «дельта ікс»). Таким чином, ∆х = х1 - х0, звідки випливає, що х1 = х0 + ∆х. Кажуть також, що початкове значення аргументу х0 одержало приріст ∆х. Внаслідок цього значення функції зміниться на величину f(х1) - f(х0). Ця різниця називається приростом функції в точці х0, відповідним до приросту ∆х, і позначається символом ∆у (читається: «дельта ігрек») або ∆f (читається: «дельта эф»). ∆у = ∆f(x) = f(х1) - f(х0) ∆у = f(х0 + ∆х) - f(х0). |
2. Задачі, які приводять до поняття похідної
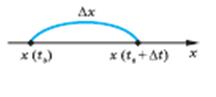
- Миттєва швидкість руху точки вздовж прямої
| х(t) – координата х точки в момент часу t
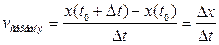
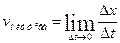
|
- Дотична до графіка функції
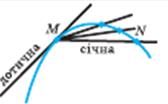
| Дотичною до кривої в даній точці М називається граничне положення січної MN. | |||
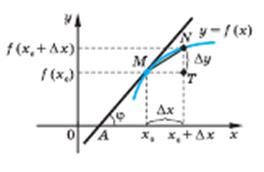
| Коли точка N наближається до точки М (рухаючись по графіку функції у = f(х)), то величина кута NМТ наближається до величини кута 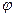 нахилу дотичної МА до осі Ох.
Оскільки tg нахилу дотичної МА до осі Ох.
Оскільки tg 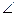 NМТ = NМТ = 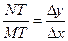 , то
tg , то
tg 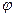 = = 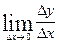
|
- Означення похідної
у = f(х)
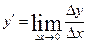
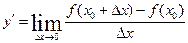
| Похідною функції у = f(х) у точці х0 називається Границя відношення приросту функції в точці х0 до приросту аргументу, коли приріст аргументу прямує до нуля. Операція знаходження похідної називається диференціюванням. |
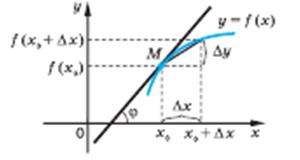
- Геометричний зміст похідної
| Значення похідної в точці х0 дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою х0 і дорівнює кутовому коефіцієнту цієї дотичної.
(Кут відлічується від додатного напрямку осі Ох проти годинникової стрілки)
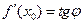 k - кутовий коефіцієнт дотичної
k - кутовий коефіцієнт дотичної
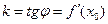
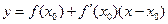 - рівняння дотичної до графіка функції - рівняння дотичної до графіка функції  у точці з абсцисою х0 у точці з абсцисою х0
|
- Механічний зміст похідної
| Похідна характеризує швидкість зміни функції при зміні аргументу | |
| S = S (t) – залежність пройденого шляху від часу V = S ′(t) – швидкість прямолінійного руху a = v′(t) – прискорення прямолінійного руху | Зокрема, похідна за часом є мірою швидкості зміни відповідної функції, що може застосовуватися до найрізноманітніших фізичних величин. Наприклад, миттєва швидкість v нерівномірного прямолінійного руху є похідна функції, яка виражає залежність пройденого шляху s від часу t. |
- Зв'язок між диференційованістю і неперервністю функції
| Якщо функція f(х) диференційована в точці х0, то вона неперервна в цій точці. |
| Якщо функція f(х) диференційована на проміжку (тобто в кожній його точці), то вона неперервна на цьому проміжку |
Дата добавления: 2015-08-26; просмотров: 4557;