Тема. Похідна тригонометричних функцій
План
- Похідна тригонометричних функцій.
- Функція синус має похідну в будь-якій точці
(sin x)′ = cos x
- Функція косинус має похідну в будь-якій точці
(cos x)′ = - sin x
- Функція тангенс має похідну в будь-якій точці
(tg x)′ =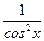 
- Функція котангенс має похідну в будь-якій точці
(ctg x)′ = -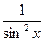 
- Формула диференціювання складної функції
(sin (аx + b))′ = a cos (аx + b)
(sin u)′ = cos u ∙ u'
(cos u)′ = - sin u ∙ u'
(tg u)′ =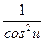 
∙ u′
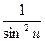(ctg u)′ = - 
∙ u′
Приклад 1. Знайти похідну функції у = sin x + cos x + tg x + 5.
Розв’язання: у' = (sin x)′ + (cos x)′ + (tg x)′ + (5)′ = cos x - sin x + .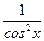
Приклад 2. Знайти похідну функції у = х3 sin x.
Розв’язання: у' = (х3)′ sin x + (sin x)′ х3 = 3х2 sin x + х3 cos x.
Приклад 3. Знайти похідну функції у = 10 ctg x + 5 cos x + х6 tg x.
Розв’язання: у' = 10 (ctg x)′+ 5 (cos x)′+ (х6)′tg x + (tg x)′х6 =
= - 10 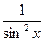- 5 sin x + 6х5 tg x + х6 =
= - 
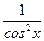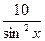- 5 sin x + 6х5 tg x + 
.
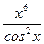Приклад 4. Знайти похідну функції у =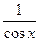 
.
Розв’язання: у' = - 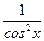(cos x)′= 
= 
.
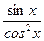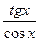Дата добавления: 2015-08-26; просмотров: 5737;