Тема. Дотична до графіка функції. Рівняння дотичної до графіка функції.
План
- Дотична до графіка функції.
- Рівняння дотичної до графіка функції.
| 1. Дотична до графіка функції | ||||||||||
Наочне уявлення про дотичну до кривої можна отримати, виготовивши криву з цупкого матеріалу (наприклад, з дроту) і прикладаючи до кривої лінійку у вибраній точці (рис.1). Якщо ми зобразимо криву на папері, а потім будемо вирізати фігуру, обмежену цією кривою, то ножиці теж будуть напрямлені по дотичній до кривої.
Спробуємо перекласти наочне уявлення про дотичну на більш точну мову.
Нехай задана деяка крива і точка М на ній (рис.2) Візьмемо на цій прямій іншу точку N і проведемо пряму через точки М і N. Цю пряму звичайно називають січною. Почнемо наближати точку N до точки М. Положення січної МN буде змінюватися, але при наближенні точки N до точки М воно почне стабілізуватися.
Дотичною до кривої в даній точці М називається граничне положення січної МN.
|
Рис. 1 Рис.2
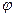нахилу дотичної до осі Ох.
Нехай точка N (через яку проходить січна МN) має абсцису х0 + ∆х. Коли точка N, рухаючись по графіку функції у = f(x), наближається до точки М (це буде при 
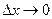), то величина кута NМТ наближається до величини кута 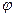нахилу дотичної МА до осі Ох. Оскільки 
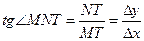, то при 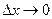значення 
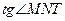наближається до 
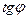, тобто
 |
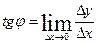
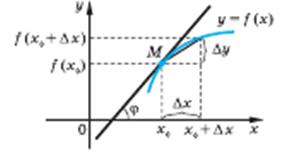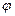нахилу дотичної в точці М з абсцисою х0 обчислюється за формулою 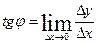. З іншого боку, 
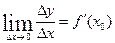. Тоді 
.
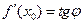Нагадаємо, що в рівнянні прямої у = kх + b кутовий коефіцієнт k дорівнює тангенсу кута 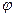нахилу прямої до осі Ох (кут відлічується від додатного напрямку осі Ох проти годинникової стрілки). Отже, якщо k – кутовий коефіцієнт дотичної, то 
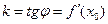. Тобто значення похідної в точці х0 дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою х0 і дорівнює кутовому коефіцієнту цієї дотичної.
Таким чином, якщо у = kх + b – рівняння дотичної до графіка функції у = f(x) у точці М з абсцисою х0 і ординатою f(x0)), то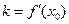 
. Тоді рівняння дотичної можна записати так: у = 
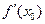· х + b. Щоб знайти значення b, врахуємо, що ця дотична проходить через точку М (х0; f(x0)). Отже, координати точки М задовольняють останньому рівнянню, тобто f(x0) = 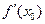· х0 + b. Звідси
b = f(x0) - 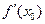· х0, і рівняннядотичної матиме вигляд
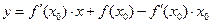. Його зручно записати так:
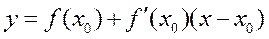Це рівняння дотичної до графіка функції у = f(x)
у точці з абсцисою х0.
Дата добавления: 2015-08-26; просмотров: 2233;