Тема. Похідна показникової та логарифмічної функцій

План

1. Похідна показникової функції.
2. Похідна логарифмічної функції.

1.Похідна показникової функції

1. Число е. У попередніх пунктах графіки показникової функції зображалися у вигляді прямих ліній ( без зламів), до яких у кожній точці можна провести дотичну. Але існування дотичної до графіка функції в точці з абсцисою х_о рівносильне її диференційованості в х_о. Тому природно припустити, що показникова функція диференційована у всіх точках області визначення.

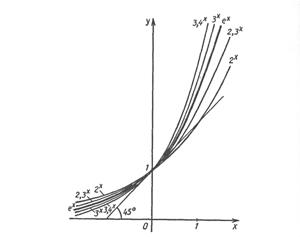Намалюємо декілька графіків функції у = а^х для а, рівного 2; 2,3; 3; 3,4 (рис. 1), і проведемо до них дотичні в точці з абсцисою 0. Кути нахилу цих дотичних до осі абсцис приблизно рівні 35°, 40°, 48° і 51° відповідно, тобто зі зростанням а кутовий коефіцієнт дотичної до графіка функції у = а^х у точці М (0; 1) поступово збільшується від tg 35° до tg 51°. Представляється очевидним, що, збільшуючи а від 2 до 3, ми знайдемо таке значення а, при яких кутовий коефіцієнт відповідної дотичної рівний 1 ( тобто кут нахилу рівний 45°). Ось точне формулювання цієї пропозиції (ми ухвалюємо без доказу):

Існує таке число, більше 2 і менше 3 (це число позначають буквою е), що показникова функція у = е^х у точці 0 має похідну, рівну 1.

Зауваження. Доведено, що число е ірраціональне, тому записується у вигляді нескінченного десяткового неперіодичного дробу. За допомогою електронних обчислювальних машин знайдене більш двох тисяч десяткових знаків числа е. Перші знаки такі: е = 2,718281828459045... .

Функцію е^х часто називають експонентою.

Формула похідної показникової функції.