Тема. Похідні елементарних функцій . Правила диференціювання функцій
План
- Похідні елементарних функцій.
- Правила диференціювання функцій.
| 1. Похідні елементарних функцій | |||
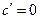
| 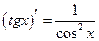
| ||
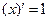 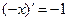
| 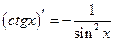
| ||
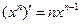
| 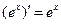
| ||
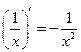 , х , х 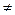 0 0
| 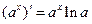 , a > 0, a - стала , a > 0, a - стала
| ||
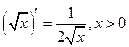
| 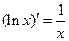 , , 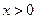
| ||
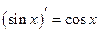
| 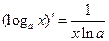 , , 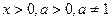 ,
a - стала ,
a - стала
| ||
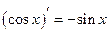
| 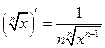 на ОДЗ правої частини формули
на ОДЗ правої частини формули
| ||
| 2. Правила диференціювання функцій | |||
| Правило | Приклад | ||
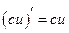 Сталий множник можна виносити за знак похідної
Сталий множник можна виносити за знак похідної
| 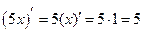
| ||
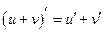 Похідна суми диференційованих функцій дорівнює сумі їх похідних
Похідна суми диференційованих функцій дорівнює сумі їх похідних
| 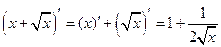
| ||
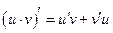
| 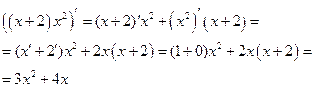
| ||
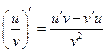
| 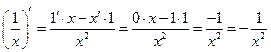
|
Вправи
- Для функції у = 2х знайдіть приріст функції ∆у, який відповідає приросту аргументу ∆х у точці х0, якщо:
1) х0 = 2 і ∆х = 3; 2) х0 = 1,5 і ∆х = 3,5; 3) х0 = 0,5 і ∆х = 2,5.
- Знайдіть приріст ∆у, який відповідає приросту аргументу ∆х у точці х0 для функції:
1) у = 3х; 2) у = х3; 3) у = х2 – х.
- Користуючись схемою обчислення похідної, знайдіть похідну функції:
1) у = 3х; 2) у = -5х; 3) у = х3.
- Знайдіть похідну функції:
1) у = х8;
2) у = х -5;
3) у = х  ;
;
4) у = х20;
5) у = х -20;
6) у = х 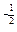 ;
;
7) у = х + 3;
8) у = х5 - х;
9) у = 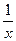 - х3;
- х3;
10) у = х2 + 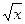 ;
;
11) у = 2х3 + 3х;
12) f(x) = х2 +5x + 2;
13) f(x) = х4 - 2x2 - 1;
14) f(x) = 2 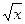 + 4х3 + 3;
+ 4х3 + 3;
15) f(x) = х5 + 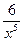 ;
;
16) f(x) = х2 + 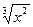 ;
;
17) f(x) = 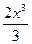 - 3х2 + 6х – 1.
- 3х2 + 6х – 1.
- Знайдіть похідну функції:
1) у = x2(х + 2);
2) у = x2(2х + х4);
3) у = (2х - 1)(1 - x2);
4) у = (3 + х3)(2 - x);
5) у = (х9 + 11)(х2 - 4);
6) у = 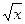 (х8 - 2);
(х8 - 2);
7) у = 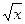 (3х2 - х);
(3х2 - х);
8) у = (х2 - 1)(x5 + 2);
9) у = 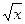 (2х + 9);
(2х + 9);
10) у = (х3 + 16) 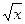 ;
;
11) у = 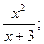
12) у = 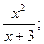
13) у = 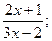
14) у = 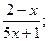
15) у = 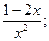
16) у = 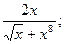
17) у = 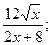
18) у = 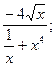
19) у = 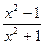 .
.
- Обчислити значення похідної f(x) у зазначених точках:
1) f(x) = х2 +2x, х = -2; х = 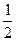 ;
;
2) f(x) = х4 - 4x, х = 2; х = -1;
3) f(x) = 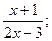 , х = 0; х = -3;
, х = 0; х = -3;
4) f(x) = 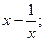 , х = -
, х = - 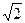 ; х = 0,1.
; х = 0,1.
- Знайдіть значення х, для яких похідна функції дорівнює нулю:
1) f(x) = 3х2 - 6x;
2) f(x) = 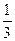 х3 + х2 + 5;
х3 + х2 + 5;
3) f(x) = 12х + 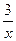 ;
;
4) f(x) = 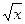 - 2х2.
- 2х2.
- Розв'язати нерівність
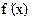 < 0, якщо:
< 0, якщо:
1) f(x) = 2х – х2; 2) f(x) = х3 + 3х2; 3) f(x) = 2х + 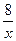 ; 4) f(x) =
; 4) f(x) = 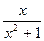 .
.
- Знайдіть похідну в точці х = 1 наступних функцій:
1) f(x) = 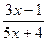 ;
;
2) f(x) = 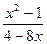 ;
;
3) f(x) = 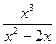 ;
;
4) f(x) = 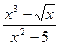 ;
;
5) f(x) = 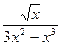 ;
;
6) f(x) = 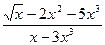 .
.
Дата добавления: 2015-08-26; просмотров: 2111;
