Тема. Границя функції в точці та на проміжку. Властивості границь. Неперервність функції в точці та на проміжку. Властивості неперервних функцій
План
- Границя функції в точці та на проміжку.
- Властивості границь.
- Неперервність функції в точці та на проміжку.
- Властивості неперервних функцій.
1. Поняття границі функції в точці.
Нехай задано деяку функцію, наприклад, f(x) = 2х – 1. Розглянемо графік цієї функції та таблицю її значень у точках, які на числовій прямій розташовані достатньо близько до числа 2.
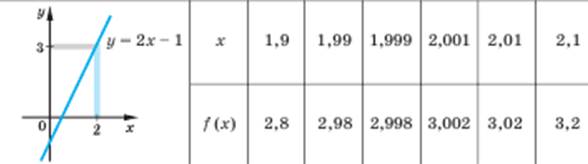 |
З таблиці та графіка видно, що чим ближче аргумент х до числа 2 (це позначають х 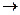 2 і кажуть, що х прямує до 2), тим ближче значення функції f(x) = 2х – 1 до числа 3 (позначають f(x)
2 і кажуть, що х прямує до 2), тим ближче значення функції f(x) = 2х – 1 до числа 3 (позначають f(x) 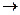 3 і кажуть, що f(x) прямує до 3). Це записують також так:
3 і кажуть, що f(x) прямує до 3). Це записують також так: 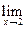 (2х – 1) = 3 (читається: «Ліміт 2х – 1 при х, що прямує до 2, дорівнює 3» і кажуть, що границя функції 2х – 1 при х, що прямує до 2 (або границя функції в точці 2), дорівнює 3.
(2х – 1) = 3 (читається: «Ліміт 2х – 1 при х, що прямує до 2, дорівнює 3» і кажуть, що границя функції 2х – 1 при х, що прямує до 2 (або границя функції в точці 2), дорівнює 3.
У загальному випадку запис 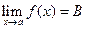 означає, що при
означає, що при 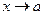
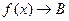 , тобто В – число, до якого прямує значення функції f(x), коли х прямує до а.
, тобто В – число, до якого прямує значення функції f(x), коли х прямує до а.
Запис позначень 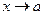 і
і 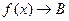 за допомогою знака модуля
за допомогою знака модуля
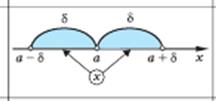
| Позначення і його зміст | Ілюстрації | Запис за допомогою модуля |
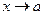 На числовій прямій точка ч знаходиться від точки а на малій відстані (менше
На числовій прямій точка ч знаходиться від точки а на малій відстані (менше 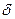 ) )
| 
| 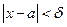
|
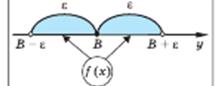
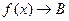 Значення
Значення 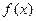 на числовій прямій знаходиться на малій відстані від В ( менше на числовій прямій знаходиться на малій відстані від В ( менше 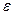 ) )
| 
| 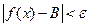
|
| Означення границі функції в точці | ||
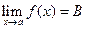
| Число В називається границею функції f(x) у точці а (при х, що прямує до а), якщо для будь-якого додатного числа 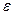 знайдеться таке додатне число знайдеться таке додатне число 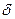 , що при всіх х , що при всіх х 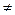 а, які задовольняють нерівності а, які задовольняють нерівності 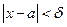 , виконується нерівність , виконується нерівність 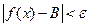
|
2. Властивості границь
| Зміст правил граничного переходу | Запис і формулювання правил граничного переходу |
Якщо f(x) = c, то при 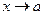 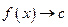
| 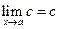 Границя сталої функції дорівнює цій самій сталій
Границя сталої функції дорівнює цій самій сталій
|
Якщо при 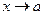
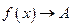 і і 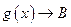 , то , то 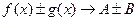
| 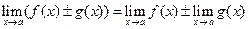 Границя суми (різниці) двох функцій дорівнює сумі (різниці) їх границь, якщо границі доданків існують
Границя суми (різниці) двох функцій дорівнює сумі (різниці) їх границь, якщо границі доданків існують
|
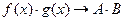
| 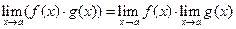 Границя добутку двох функцій дорівнює добутку їх границь, якщо границі множників існують
Границя добутку двох функцій дорівнює добутку їх границь, якщо границі множників існують
|
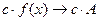
| 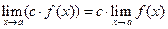 Сталий множник можна виносити за знак границі
Сталий множник можна виносити за знак границі
|
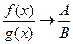 (де В (де В 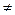 0) 0)
| 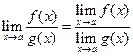 (де (де 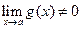 )
Границя частки двох функцій дорівнює частці їх границь, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю )
Границя частки двох функцій дорівнює частці їх границь, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю
|
3. Неперервність функції в точці та на проміжку
Функція f(x) називається неперервною в точці а, якщо при 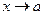
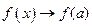 , тобто
, тобто
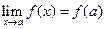
4. Властивості неперервних функцій
Якщо функція f(x) неперервна в кожній точці деякого проміжку І, то її називають неперервною на проміжку І.
Якщо функції f(x) і g(x) неперервні в точці а, то сума, добуток і частка неперервних в точці а функцій неперервні в точці а (частка у випадку, коли дільник g(x) 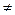 0 )
0 )
Графік функції, неперервної на проміжку, - нерозривна лінія на цьому проміжку.
Всі елементарні функції неперервні в кожній точці своєї області визначення, тому на кожному проміжку з області визначення їх графіки – нерозривні лінії.
Якщо на інтервалі 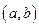 функція f(x) неперервна і не перетворюється на нуль, то вона на цьому інтервалі зберігає сталий знак.
функція f(x) неперервна і не перетворюється на нуль, то вона на цьому інтервалі зберігає сталий знак.
Вправи
- Розкрити зміст нерівності
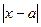 <
< 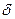 .
. - Як зобразити
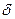 - околицю точки а = - 2, якщо
- околицю точки а = - 2, якщо 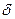 = 0,5.
= 0,5. - Розв'язати рівняння та нерівності:
1) 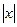 = 4;
= 4;
2) 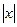 = 0;
= 0;
3) 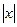 = -6;
= -6;
4) 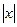 = х;
= х;
5) 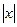 = -х;
= -х;
6) 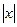 > 0;
> 0;
7) 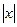 < 0;
< 0;
8) 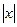
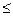 2;
2;
9) 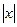 > 7;
> 7;
10) 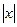
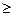 -5.
-5.
- Чи є неперервною в кожній із точок х = -1, х = 1, х = 3 функція, графік якої зображено на рис 1
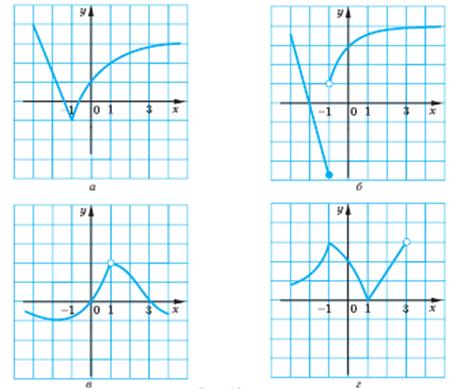 |
Рис. 1
- Чи є функція безперервною в кожній точці даного проміжку?
1) f (x) = x5 – 3x2 + 2, (- 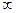 ; +
; + 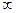 );
);
2) f (x) = 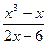 , [5; +
, [5; + 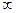 );
);
3) f (x) = 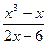 , (0; +
, (0; + 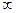 ).
).
4) f (x) = x2 – 3x, (- 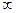 ; +
; + 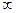 );
);
5) f (x) = 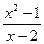 , (0; +
, (0; + 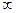 );
);
6) f (x) = 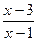 , [2; +
, [2; + 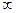 ).
).
- З'ясувати, до якого числа прагне функція f (x), якщо
1) f (x) = 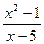 при х
при х 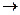 0;
0;
2) f (x) = x2 – 5x + 1 при х  1;
1;
3) f (x) = 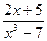 при х
при х  2;
2;
4) f (x) = 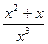 при х
при х 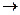 -1;
-1;
5) f (x) = 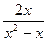 при х
при х 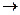 3.
3.
- Знайти: 1)
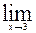 ( x3 + 2x - 1); 2)
( x3 + 2x - 1); 2) 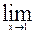
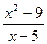 ; 3)
; 3) 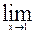
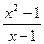 .
. - Дослідити функцію f (x) =
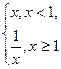 у точці х0 = 1.
у точці х0 = 1. - Дослідити функцію f (x) =
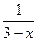 , х
, х 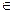 R, x
R, x 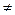 3 на безперервність у точці х = 3.
3 на безперервність у точці х = 3. - Дослідити функцію на безперервність у точках х = 0, х = -1, х = 1, якщо f (x) =
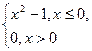
- Знайти:
1) 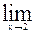 ( x2 + x +5);
( x2 + x +5);
2) 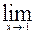 (4x –x3);
(4x –x3);
3) 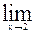 ( x2 + 3x -5);
( x2 + 3x -5);
4) 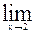
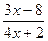 ;
;
5) 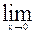
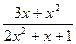 ;
;
6) 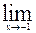
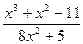 ;
;
7) 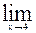 ( x4 - 2x + 5);
( x4 - 2x + 5);
8) 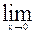
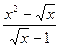 .
.
9) 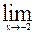
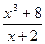 ;
;
10) 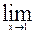
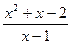 ;
;
11) 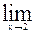
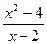 ;
;
12) 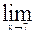
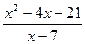 ;
;
13) 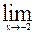
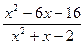 ;
;
14) 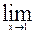
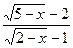 ;
;
15) 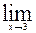
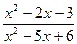 ;
;
16) 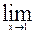
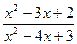 ;
;
17) 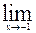
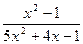 ;
;
18) 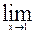
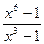 ;
;
19) 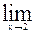
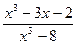 ;
;
20) 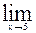
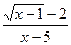 ;
;
21) 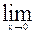
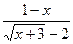 ;
;
22) 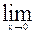
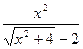 ;
;
23) 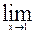
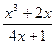 ;
;
24) 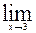
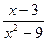 ;
;
25) 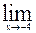
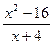 .
.
Дата добавления: 2015-08-26; просмотров: 3052;
