Потенціальне векторне поле
Розглянемо плоске векторне поле 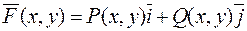 .
.
Нехай у деякій однозв'язній області D поля виконується умова 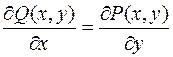 .
.
Тоді вираз P(x,y)dx+Q(x,y)dy є повним диференціалом деякої функції u=u(x,y), тобто 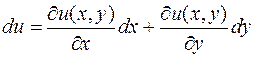 ,
,
де 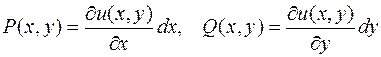 .
.
Але тоді задане векторне поле можна записати так:
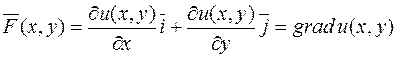 .
.
Означення. Векторне поле  зветься потенціальним, якщо воно є градієнтом деякого скалярного поля u:
зветься потенціальним, якщо воно є градієнтом деякого скалярного поля u: 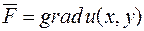 .
.
Скалярна функція u зветься потенціалом векторного поля  .
.
Іноді перед градієнтом ставиться знак "-", що не має принципового значення, а лише відповідає конкретному фізичному змісту. Наприклад, для електростатичного поля 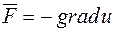 означає, що в напрямку вектора напруги електричного поля
означає, що в напрямку вектора напруги електричного поля  електричний потенціал спадає.
електричний потенціал спадає.
Як бачимо, умова 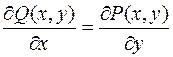 в потенціальному полі рівнозначна існуванню повного диференціала. Відповідно, задача відшукання повного диференціала рівнозначна задачі обчислення потенціалу векторного поля.
в потенціальному полі рівнозначна існуванню повного диференціала. Відповідно, задача відшукання повного диференціала рівнозначна задачі обчислення потенціалу векторного поля.
Зазначимо, що потенціал векторного поля обчислюється з точністю до довільної сталої на підставі того, що grad(u+c)=gradu.
Приклад. Пересвідчитись, що векторне поле
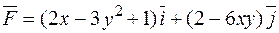 потенціальне і знайти його потенціал.
потенціальне і знайти його потенціал.
Розв'язання. P(x,y)=2x-3y2+1
Q(x,y)=2-6xy

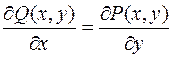 свідчить про те, що поле потенціальне. Потенціал векторного поля дорівнює циркуляції цього поля по деякій лінії L
свідчить про те, що поле потенціальне. Потенціал векторного поля дорівнює циркуляції цього поля по деякій лінії L 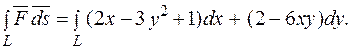
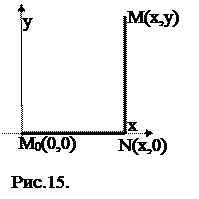 Шлях інтегрування L виберемо так:
Шлях інтегрування L виберемо так:
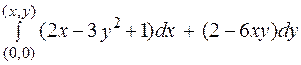 =
=
по відрізку M0N: y=0; dy=0
по відрізку NM: x=const; dx=0
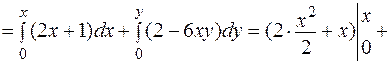
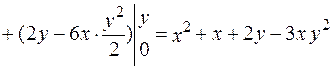
Отже, u(x,y)=x2+x+2y-3xy2+C (C=const).
Розглянемо просторове векторне поле
 .
.
Якщо векторне поле 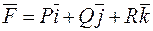 потенціальне, а u=u(x,y,z) ‑ його потенціал, то
потенціальне, а u=u(x,y,z) ‑ його потенціал, то 
У потенціальному векторному полі циркуляція не залежить від шляху інтегрування, а лише від початкової і кінцевої точок M0(x0;y0;z0) та M(x;y;z):
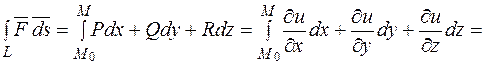
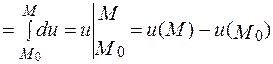 .
.
Приклад. Знайти циркуляцію градієнта скалярного поля u=xy по відрізку прямої, яка з'єднує точки A(1;1) та B(2;2).
Розв'язання: 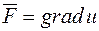 , тоді
, тоді
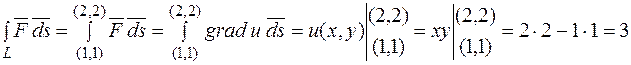
Циркуляцією градієнта скалярного поля є різниця потенціалів цього поля.
Для потенціального поля справедлива теорема, яка відповідає розглянутим раніше властивостям криволінійного інтегралу:
Теорема. Наступні чотири властивості векторного поля  , заданого в однозв’язній області
, заданого в однозв’язній області 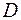 , еквівалентні:
, еквівалентні:
1. циркуляція поля  по будь-якому замкненому контуру, розміщеному в області
по будь-якому замкненому контуру, розміщеному в області 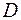 , дорівнює нулю;
, дорівнює нулю;
2. циркуляція поля  впродовж довільної кривої
впродовж довільної кривої 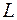 (яка лежить в області
(яка лежить в області 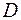 ) з початком в точці А та кінцем в точці В залежить тільки від положення точок А та В і не залежить від форми кривої;
) з початком в точці А та кінцем в точці В залежить тільки від положення точок А та В і не залежить від форми кривої;
3. існує функція 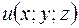 така, що
така, що 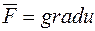 ;
;
4. поле  є безвихорним, тобто
є безвихорним, тобто 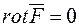 .
.
Дата добавления: 2015-07-22; просмотров: 2635;
