Енергія пружних хвиль. Потік і густина потоку енергії хвиль
Нехай в деякому пружному середовищі в напрямі осі х поширюється плоска поздовжня хвиля
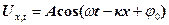 . (24)
. (24)
Виділимо в цьому середовищі елементарний об’єм ΔV, настільки
малий, щоб швидкість хвилі 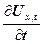 і швидкість деформації
і швидкість деформації 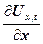 у всіх
у всіх
його точках були однакові.
Повну механічну енергію, локалізовану у виділеному об’ємі, можна розрахувати за формулою
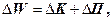
де 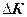 - кінетична енергія виділеного об’єму;
- кінетична енергія виділеного об’єму;
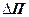 - потенціальна енергія пружної деформації цього об’єму.
- потенціальна енергія пружної деформації цього об’єму.
Кінетичну енергію, яку має виділений об’єм пружного середовища знаходимо за формулою
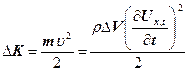 , (25)
, (25)
де ρ - густина середовища виділеного об’єму.
Першу похідну за часом виразу (24) підставимо в (25), одержимо
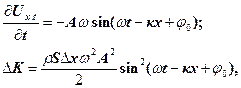 (26)
(26)
де 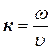 ─ хвильове число.
─ хвильове число.
У відповідності з рис. 4 потенціальну енергію пружної деформації виділеного об’єму знаходимо так:
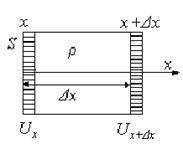
Рис. 4
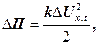 (27)
(27)
де k – коефіцієнт пружності середовища, який відповідно до закону Гука (8) дорівнює 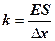 ;
;
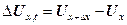 ─ величина деформації виділеного об’єму пружного середовища.
─ величина деформації виділеного об’єму пружного середовища.
З урахуванням цих позначень (27) матиме вигляд
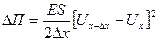 . (28)
. (28)
Помножимо й поділимо (28) на Δх2, одержимо
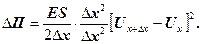 (29)
(29)
В граничному випадку при Δх=0 одержуємо
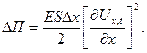 (30)
(30)
Підставимо у формулу (30) значення модуля Юнга 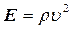 , і швидкість деформації
, і швидкість деформації 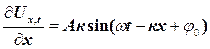 , одержимо
, одержимо
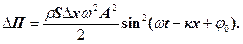 (31)
(31)
Повну енергію, локалізовану у виділеному об’ємі пружного середовища, одержимо при додаванні кінетичної енергії (26) і потенціальної енергії (31)
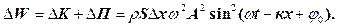 (32)
(32)
Якщо врахувати, що середнє значення квадрата синуса за час в один період дорівнює 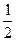 , то одержимо середнє значення повної енергії, яке буде дорівнювати
, то одержимо середнє значення повної енергії, яке буде дорівнювати
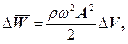 (33)
(33)
де ΔV=SΔx – елементарний об’єм пружного середовища.
Середнє значення густини енергії легко одержати, якщо (33) поділити на величину виділеного об’єму пружного середовища
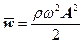 . (34)
. (34)
Нехай через площадку S (рис.4), яка є перпендикулярною до напрямку поширення хвилі, за час Δt переноситься енергія ΔW. Тоді вектор густини енергії буде дорівнювати
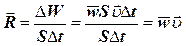 , (35)
, (35)
де 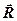 ─ вектор густини потоку енергії;
─ вектор густини потоку енергії;
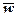 ─ середня густина перенесеної хвилями енергії;
─ середня густина перенесеної хвилями енергії;
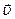 ─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно перенесення енергії.
─ вектор швидкості, модуль якої дорівнює фазовій швидкості хвиль з напрямком поширення хвиль і відповідно перенесення енергії.
Вектор потоку енергії 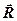 вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова.
вперше одержав і розглянув видатний російський фізик Умов. На честь цього фізика він був названий вектором Умова.
Дата добавления: 2015-08-26; просмотров: 1610;
