Б) количество теплоты, подведенное к потоку воздуха в камере сгорания

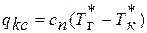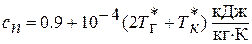, где - средняя условная теплоемкость процесса подвода теплоты в камере сгорания

в) работа, развиваемая турбиной на её валу .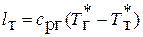

1.16. Уравнение неразрывности.

Рассматривается открытая термодинамическая система - поток жидкости или газа. Необходимо определить условия изменения массы рабочего тела при его течении в изолированном канале с твердыми стенками.

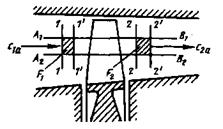
С этой целью выделим струйку тока из потока жидкости (рис.1.19) и два

нормальных сечения к её средней линии «1-1» и «2-2».

Рис.1.19. К выводу уравнения неразрывности.

За время 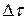каждое из сечений перемещается и занимает положение «1^’-1^’» и «2^’-2^’». Определим массу газа между сечениями «1-1» - «1^’-1^’» и «2-2» - «2^’-2^’»: ;

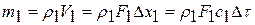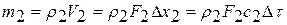
Принимаем, что поток стационарный, то есть изменение параметров потока не зависит от времени, а также равенство масс т₁ и т₂. Тогда разделив на 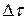, получаем уравнение неразрывности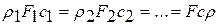

Подставляя размерности величин в эту формулу, получаем уравнение секундного расхода массы газа:

Из формулы для расхода газа следует, что он может уменьшиться, если:

а) уменьшается площадь проходного сечения F, например, при попадании посторонних предметов на вход в двигатель;

б) снижается скорость с , например, при увеличении угла атаки полета самолета уменьшается составляющая скорости полета на входе в двигатель;

в) уменьшается плотность 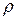, например, при попадании горячих струй газа на вход в двигатель. В результате температура воздуха растет, а плотность падает согласно уравнению состояния 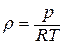- «тепловое дросселирование».

Разделив и умножив уравнение расхода на плотность тока при критическом режиме течения 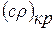, получим уравнение расхода в следующем виде: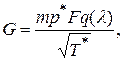

где 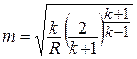; 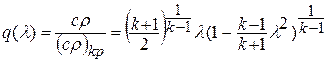- относительная плотность тока. При умеренных температурах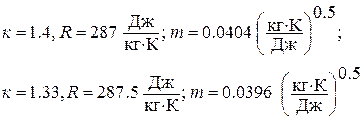

1.17. Уравнение первого закона термодинамики для открытой

термодинамической системы.

Согласно первому закону термодинамики сообщенное количество теплоты рабочему телу в закрытой термодинамической системе (например,

газ, находящийся в цилиндре поршневого двигателя) идет на увеличение внутренней энергии и на совершение деформационной работы и в дифференциальной форме имеет вид: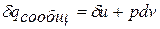

В открытой термодинамической системе (поток воздуха по тракту газотурбинного двигателя) это уравнение преобразуется к виду:

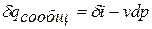
Интегрируя это уравнение от сечения «1-1» до «2-2», получаем:

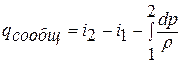
Здесь интеграл в общем случае называют политропной работой или работой расширения (сжатия) против сил давления в движущемся газе.

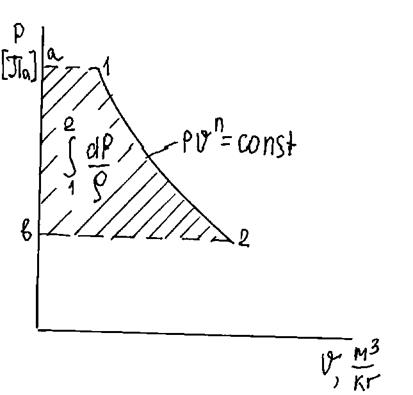
В 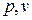- координатах политропная работа изображается площадью 1аb2 (рис.1.20). При отсутствии теплообмена между рабочим телом и внешней средой ( 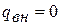) и трения ( 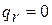) интеграл представляет собой адиабатную работу, которая численно равна изменению энтальпии рабочего тела между сечениями потока:

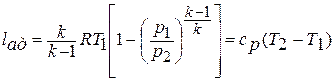
Рис.1.20. Политропная работа в 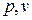координатах

Практический интерес представляет процесс без внешнего теплообмена, но с наличием трения (используется, например, для изучения рабочего процесса в ступени компрессора). Для этого случая, имея в виду, что 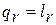, уравнение первого закона термодинамики можно привести в следующему виду:

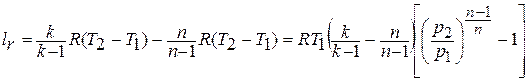
1.18. Обобщенное уравнение Даниила Бернулли (1700 – 1782),

швейцарского академика.

Напишем два уравнения:

1) уравнение сохранения энергии

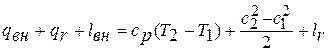
2) уравнение первого закона термодинамики

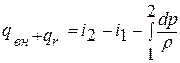
Принимая, что теплоемкость с_р не зависит от температуры, вычитаем из первого уравнения второе. В результате получаем обобщенное уравнение Д.Бернулли: ,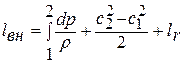

которое гласит: подведенная извне работа расходуется на создание политропной (технической) работы, на приращение кинетической энергии потока и на преодоление сил трения (гидравлических сопротивлений).

Внешний вид уравнения Д.Бернулли не зависит от теплообмена с окружающей средой ( 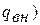. Однако теплообмен оказывает влияние на параметры в конце политропного процесса (через показатель политропы). Например, чем больше показатель политропы отличается от показателя адиабаты, тем больше теплоты подводится к потоку газа.

Если к потоку газа внешняя работа не подводится ( 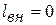), трением можно пренебречь ( 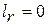), а поток газа движется с небольшой скоростью ( 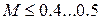), то есть изменением плотности можно пренебречь ( 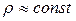), получим уравнение Д.Бернулли для несжимаемой жидкости:

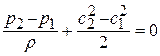или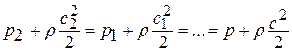

Здесь 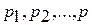- статические давления в сечениях «1-1» , «2-2» и в произвольном сечении потока. Статическим давлениемназывают давление, действующее на измерительную стенку, поставленную параллельно вектору скорости.

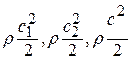- динамические давления или скоростные напоры в соответствующих сечениях потока.

Сумму статического и динамического давления в потоке газаназываютполным давлением или давлением заторможенного потока газа: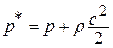

Таким образом, полным давлениемназываютдавление, действующее на измерительную стенку, поставленную перпендикулярно вектору скорости.На основании этого определения полного давления используется для измерения 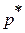трубка Пито - Прандтля, представляющая собой Г- образную трубку, повернутую навстречу потоку.

1.19. Уравнение обращения воздействия.

Прологарифмируем уравнение расхода 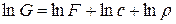, а затем его продифференцируем 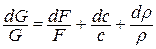, откуда найдем отношение

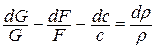
Подставляем полученное выражение в уравнение состояния, написанное в дифференциальной форме:

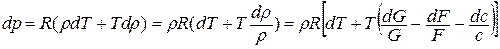
или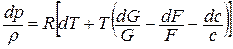

Уравнение Д.Бернулли напишем в дифференциальной форме:

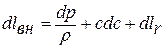
из которого находим отношение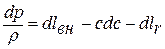

Подставляем значение 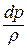в предыдущее равенство:

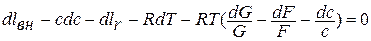
Учитывая, что 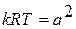, получаем:

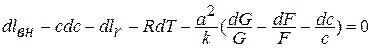
Заменяя в уравнении сохранения энергии в дифференциальной форме:

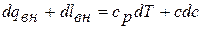
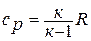и решая это уравнение относительно 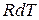, получаем:

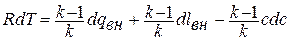
Подставляя полученное выражение в написанное выше уравнение, получаем:

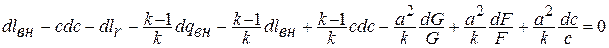
Учитывая соотношение для числа Маха 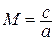, после преобразований получаем окончательно:

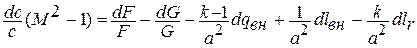
Это соотношение, установленное Л.А. Вулисом, называется условием обращения воздействия. Из соотношения следует, что, например, для увеличения скорости дозвукового потока идеального газа ( 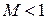, 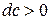) необходимы при отсутствии прочих воздействий нижеперечисленные воздействия.

Каналы, в которых происходит ускорение потока ( 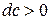), называют конфузорами или соплами.

Каналы, в которых происходит торможение потока ( 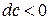), называют диффузорами.

На рис.1.18 – 1.21 показаны различные случаи воздействий для дозвукового ( 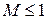) и сверхзвукового ( ) потоков: