Уравнение политропного процесса.
Продифференцируем уравнение состояния для 1 кг идеального газа:
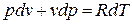
Принимая теплоемкость не зависящей от температуры, получим уравнение первого закона термодинамики в дифференциальной форме:
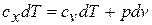
Подставляя в это уравнение выражение для 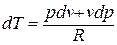 , получаем
, получаем
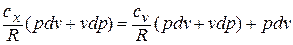
или
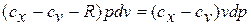
Разделяя переменные и произведя интегрирование, получаем
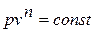 ,
,
где 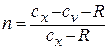 - показатель политропы, может принимать значения от нуля до бесконечности.
- показатель политропы, может принимать значения от нуля до бесконечности.
Зависимость между температурой и удельным объёмом определяется путём замены давления в уравнении политропного процесса его значением из уравнения состояния идеального газа:
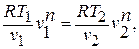
отсюда
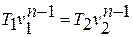 или
или 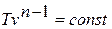
Исключая подобным же образом удельный объём, находим зависимость между давлением и температурой:
 отсюда
отсюда 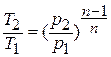 или
или 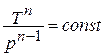
Деформационная работа, производимая 1 кг газа в политропном процессе, определяется по формуле:
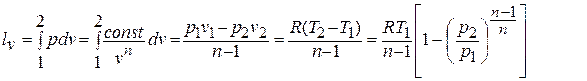 Техническая работа, производимая 1 кг газа в политропном процессе, находится по формуле:
Техническая работа, производимая 1 кг газа в политропном процессе, находится по формуле:
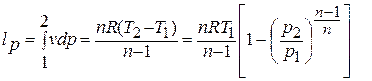
То есть отношение технической и деформационной работ равно показателю политропы:
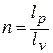
Изменение внутренней энергии в политропном процессе находится общей формулой: 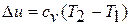
Теплоёмкость процесса 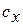 определяется из выражения для показателя политропы:
определяется из выражения для показателя политропы: 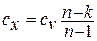
Количество теплоты в политропном процессе находится по формуле:
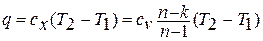
1.12. Энтальпия рабочего тела.
В термодинамике важную роль играет сумма внутренней энергии системы 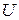 и произведения давления системы
и произведения давления системы 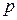 на её объём
на её объём 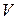 , называемая энтальпией или теплосодержанием и обозначаемая I или Н:
, называемая энтальпией или теплосодержанием и обозначаемая I или Н:
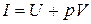
Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния.
Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).
Энтальпия обладает свойством аддитивности . Величина
i = u + pv, (1.17)
называемая удельной энтальпией ( 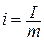 ), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:
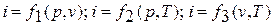 , а величина di является полным
, а величина di является полным
дифференциалом.
Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.
Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G (рис.1.7). Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил: 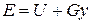 . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа:
. В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: 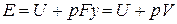 . Получаем, что
. Получаем, что  , т.е. энтальпию можно трактовать как энергию расширенной системы.
, т.е. энтальпию можно трактовать как энергию расширенной системы.
Уравнение 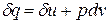 в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения
в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения 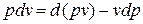 может быть записано в виде
может быть записано в виде 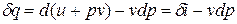 .
.
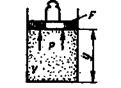
Рис.1.10. К определению физического смысла энтальпии
Из этого соотношения следует, что если давление термодинамической системы сохраняется неизменным, то есть осуществляется изобарный процесс (dp = 0), то 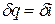 и
и 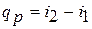 , то теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
, то теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
Это выражение очень часто используется в расчетах, так как огромное
количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбореактивных двигателей, теплообменных аппаратах), а также целый ряд процессов химической технологии и многих других производствах осуществляется при постоянном давлении. Кстати, по этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии, a не внутренней энергии.
Для идеального газа для вычисления энтальпии используется формула
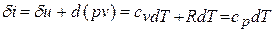
Так как между энтальпией и внутренней энергией существует связь, выбор начала отсчета одной из них произволен: в точке, принятой за начало отсчета внутренней энергии, 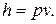 Например, для воды при
Например, для воды при  = 0,01 °С ,
= 0,01 °С ,
р = 610,8 Па,  , a
, a 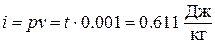 .
.
При расчетах практический интерес представляет изменение энтальпии в конечном процессе:

1.13. Энтропия рабочего тела.
Как уже указывалось, величина 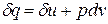 не является полным дифференциалом, так как теплота и изменение внутренней энергии зависят от теплоемкости, которая, в свою очередь, является функцией температуры. Кроме того, чтобы проинтегрировать правую часть этого уравнения, нужно знать зависимость давления от удельного объёма, то есть нужно знать процесс, который совершается.
не является полным дифференциалом, так как теплота и изменение внутренней энергии зависят от теплоемкости, которая, в свою очередь, является функцией температуры. Кроме того, чтобы проинтегрировать правую часть этого уравнения, нужно знать зависимость давления от удельного объёма, то есть нужно знать процесс, который совершается.
В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты 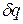 является абсолютная температура Т.
является абсолютная температура Т.
Покажем это на примере изменения состояния идеального газа в равновесных процессах: 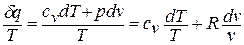
Выражение 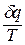 при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния, которая называется энтропией, обозначается для 1 кг газа через
при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния, которая называется энтропией, обозначается для 1 кг газа через 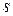 и измеряется в
и измеряется в 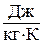 . Термин «энтропия» был введен впервые Рудольфом Юлиусом Эммануэлем Клаузиусом (1822 – 1888), немецким физиком, в 1865 году.
. Термин «энтропия» был введен впервые Рудольфом Юлиусом Эммануэлем Клаузиусом (1822 – 1888), немецким физиком, в 1865 году.
Для произвольного количества газа энтропия, обозначаемая через 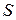 ,
,
равна 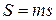 и измеряется в
и измеряется в 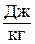 .
.
Таким образом, аналитически энтропия определяется следующим образом: 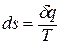
Эта формула справедлива как для идеальных, так и для реальных газов.
Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

Понятием «энтропия» (от греч. Entropia – поворот, превращение) будем называть в термодинамике направление теплообмена между рабочим телом термодинамической системы и внешней средой.
Значение энтропии для заданного состояния газа определяется интегрированием уравнения для энтропии:
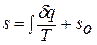 , где
, где  - константа интегрирования.
- константа интегрирования.
При температурах, близких к абсолютному нулю, все известные газы находятся в конденсированном состоянии. Вальтер Нернст (1864 – 1941), немецкий физик и химик, в 1906 году экспериментально установил, а Макс Планк (1858 – 1947), немецкий физик, в 1912 году окончательно сформулировал следующий принцип:
при температуре, стремящейся к абсолютному нулю, энтропия газа, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю,то есть 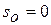 при
при 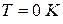 .
.
Этот закон называют третьим законом термодинамикиили тепловой теоремой В.Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.
Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:
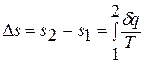 (1.18)
(1.18)
поэтому энтропию тоже отсчитывают от произвольно выбранного уровня.
Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение для энтропии, полагая 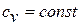 :
:

Имея в виду уравнение состояния, записанное для состояний «1» и «2», получаем: 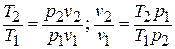
После подстановки отношений 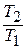 и
и 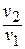 получаем следующие формулы для изменения энтропии идеального газа:
получаем следующие формулы для изменения энтропии идеального газа:
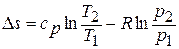 ;
; 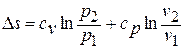
Поскольку энтропия есть функция состояния рабочего тела, написанными уравнениями можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями «1» и «2» и, в частности, от того, равновесный этот переход или нет.
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов  -диаграмму, на которой (как и
-диаграмму, на которой (как и
на 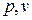 -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис.1.11).
-диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис.1.11).
Из уравнения для изменения энтропии следует, что в равновесном процессе: 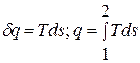 . Очевидно, что в
. Очевидно, что в  - диаграмме элементарная теплота процесса
- диаграмме элементарная теплота процесса 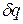 изображается элементарной площадкой с высотой
изображается элементарной площадкой с высотой 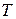 и основанием ds, а площадь, ограниченная
и основанием ds, а площадь, ограниченная

Рис.1.11. Графическое изображение теплоты в  - координатах.
- координатах.
линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
Формула для элементарного изменения энтропии показывает, что  и
и 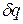 имеют одинаковые знаки, следовательно, по характеру изменения в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты (
имеют одинаковые знаки, следовательно, по характеру изменения в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты ( 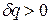 ) его энтропия возрастает (
) его энтропия возрастает ( 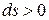 ), а при отводе теплоты (
), а при отводе теплоты (  ) убывает (ds<0). При отсутствии теплообмена
) убывает (ds<0). При отсутствии теплообмена 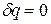 и
и 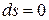 , а равновесный процесс называют адиабатным.
, а равновесный процесс называют адиабатным.
1.14. Исследование термодинамических процессов.
Изменение состояния термодинамической системы во времени называется термодинамическим процессом.
Система, выведенная из состояния равновесия и предоставленная при постоянных параметрах окружающей среды самой себе, через некоторое время вновь придёт в равновесное состояние, соответствующее этим параметрам. Такое самопроизвольное (без внешнего воздействия) возвращение системы в состояние равновесия называется релаксацией, а промежуток времени, в течение которого система возвращается в состояние равновесия, называется временем релаксации.
Термодинамический процесс называется равновесным, если все параметры системы при его протекании меняются достаточно медленно по сравнению с соответствующим временем релаксации.
Рассмотрим, например, процесс сжатия газа в цилиндре. Если время смещения поршня от одного положения до другого существенно превышает
время релаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объёму цилиндра. Это выравнивание обеспечивается непрерывным столкновением молекул, в результате чего подводимая от поршня к газу энергия достаточно быстро и равномерно распределяется между ними. Если последующее смещение поршня будет происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным.
Таким образом, равновесный процесс состоит из непрерывного ряда последовательных состояний равновесия, поэтому в каждой его точке состояние можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процессами, так как они значительно упрощают решение задачи. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа в цилиндре будет равновесным, если скорость перемещения поршня много меньше скорости звука.
1.14.1. Изобарный процесс.
Если показатель политропы п=0, то из уравнения политропного процесса находим 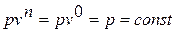 . Таким образом, политропный процесс с показателем п=0 протекает при постоянном давлении; этот процесс называется изобарным. Следовательно, меняются в процессе только температура газа и его объём, причём из уравнения состояния находим, что изменение объёма пропорционально изменению температуры (первый
. Таким образом, политропный процесс с показателем п=0 протекает при постоянном давлении; этот процесс называется изобарным. Следовательно, меняются в процессе только температура газа и его объём, причём из уравнения состояния находим, что изменение объёма пропорционально изменению температуры (первый
закон Жозефа Луи Гей-Люссака (1778 – 1850), французского химика и физика, уточненный им в 1802 году, и Жоржа Шарля (1746 – 1823), французского ученого, открытый им в 1787 году) 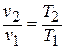 (рис. 1.12).
(рис. 1.12).
Деформационная работа в изобарном процессе определяется по формуле:
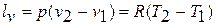
Теплоёмкость процесса
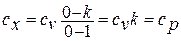
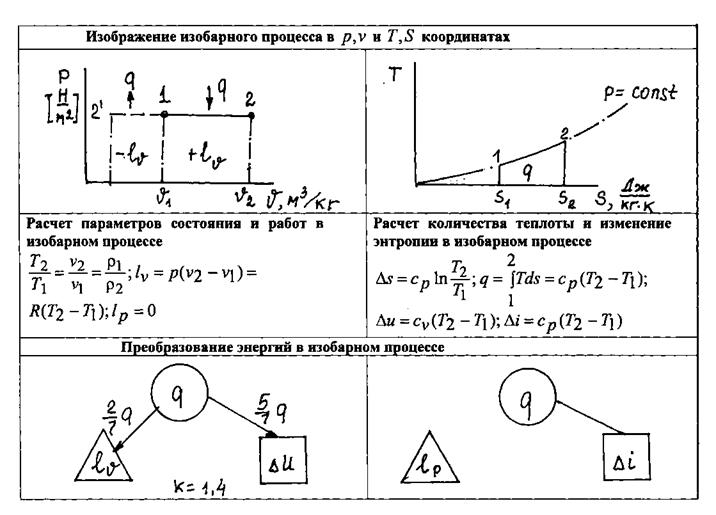
Подведенное количество теплоты

Изменение энтропии в процессе

|
Рис.1.12. Изображение изобарного процесса в различных системах
координат и преобразование энергий в этом процессе
1.14.2. Изотермический процесс.
Если показатель политропы п=1, то из уравнения политропного процесса находим 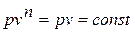 или
или 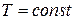 .
.
Процесс при п=1 происходит при постоянной температуре и называется изотермическим. Из уравнения состояния для начала и конца процесса получаем 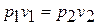 или
или 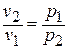 , то есть в этом процессе объёмы газа меняются обратно пропорционально давлениям (закон Роберта Бойля (1627 – 1691), английского химика и физика, и Эдма Мариотта (1620 – 1684), французского физика, установивших этот закон в 1676 году).
, то есть в этом процессе объёмы газа меняются обратно пропорционально давлениям (закон Роберта Бойля (1627 – 1691), английского химика и физика, и Эдма Мариотта (1620 – 1684), французского физика, установивших этот закон в 1676 году).
Так как температура в процессе не меняется, то внутренняя энергия газа также остается постоянной и 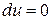 . Следовательно, уравнение первого закона термодинамики для этого процесса имеет вид
. Следовательно, уравнение первого закона термодинамики для этого процесса имеет вид 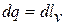 , вся подведенная теплота превращается в работу расширения газа и обратно, вся работа, затраченная на сжатие газа, должна быть отведена в окружающую среду в форме теплоты.
, вся подведенная теплота превращается в работу расширения газа и обратно, вся работа, затраченная на сжатие газа, должна быть отведена в окружающую среду в форме теплоты.
Деформационная работа в этом процессе находится по формуле:
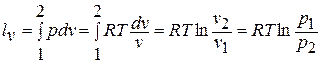
Теплоемкость процесса получается равной 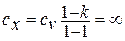
Физический смысл этой бесконечности заключается в том, что ни при каких конечных значениях теплоемкости температура газа не может быть изменена, так как вся подводимая теплота полностью превращается в работу.
На 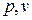 - диаграмме (рис.1.13) кривая процесса представляется равнобокойгиперболой, для которой оси координат являются асимптотами.
- диаграмме (рис.1.13) кривая процесса представляется равнобокойгиперболой, для которой оси координат являются асимптотами.
Изменение энтропии в данном процессе находится по формуле:
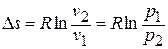

|
Рис.1.13. Изображение изотермического процесса в различных системах координат и преобразование энергий в этом процессе
1.14.3. Адиабатный процесс.
Этот процесс совершается без обмена теплотой с окружающей средой. Если показатель политропы 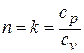 , то получим уравнение адиабатного процесса (уравнение Симеона Дени Пуассона (1781 – 1840), французского математика, механика и физика )
, то получим уравнение адиабатного процесса (уравнение Симеона Дени Пуассона (1781 – 1840), французского математика, механика и физика )
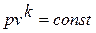
Теплоёмкость адиабатного процесса равна нулю, так как
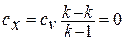 . Соответственно количество теплоты равно нулю.
. Соответственно количество теплоты равно нулю.
Из уравнения первого закона термодинамики при 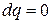 находим
находим 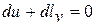 , откуда получаем
, откуда получаем 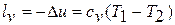 .
.
В этом процессе вся совершаемая газом деформационная работа получается за счёт уменьшения его внутренней энергии и, наоборот, вся работа, затраченная на сжатие газа, идёт на увеличение внутренней энергии.
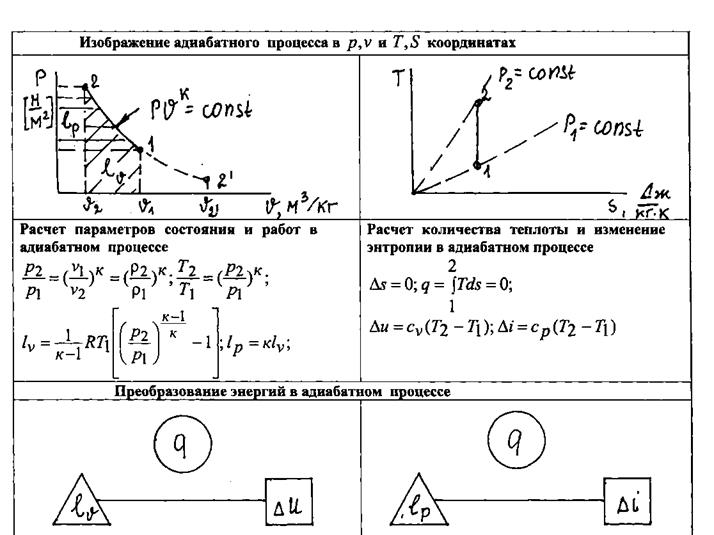
Формулы связи между параметрами газа в адиабатном процессе (рис.1.14) и формулы работы получаются из общих формул политропного процесса при условии замены в них 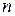 на
на 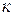 :
:
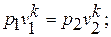

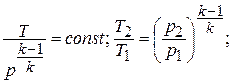
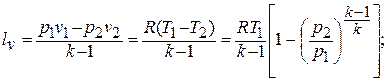
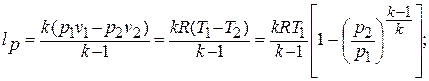
|
Рис.1.14. Изображение адиабатного процесса в различных системах координат и преобразование энергий в этом процессе
1.14.4. Изохорный процесс.
Если показатель политропы 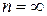 , то общую зависимость между давлением и объёмом в политропном процессе можно представить в виде
, то общую зависимость между давлением и объёмом в политропном процессе можно представить в виде 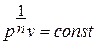 или
или 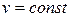 .
.
По мере увеличения показателя политропы и приближения его значения к бесконечности величина 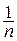 стремится к нулю; в пределе получаем
стремится к нулю; в пределе получаем 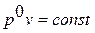 или
или 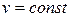 .
.
Таким образом, при показателе политропы, равном бесконечности, процесс называется изохорным(рис.1.15). Из уравнения состояния при 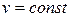 находим, что изменение состояния происходит в соответствии со вторым законом Гей-Люссака:
находим, что изменение состояния происходит в соответствии со вторым законом Гей-Люссака: 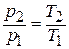
В изохорном процессе давление газа изменяется пропорционально абсолютной температуре.
Так как 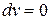 , то газ в этом процессе не совершает деформационной работы, и уравнение первого закона термодинамики приводится к виду:
, то газ в этом процессе не совершает деформационной работы, и уравнение первого закона термодинамики приводится к виду:
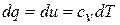
то есть все подведенное тепло идёт на увеличение внутренней энергии газа.
Изменение энтропии в изохорном процессе находится по формуле
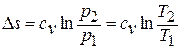 .
.
|
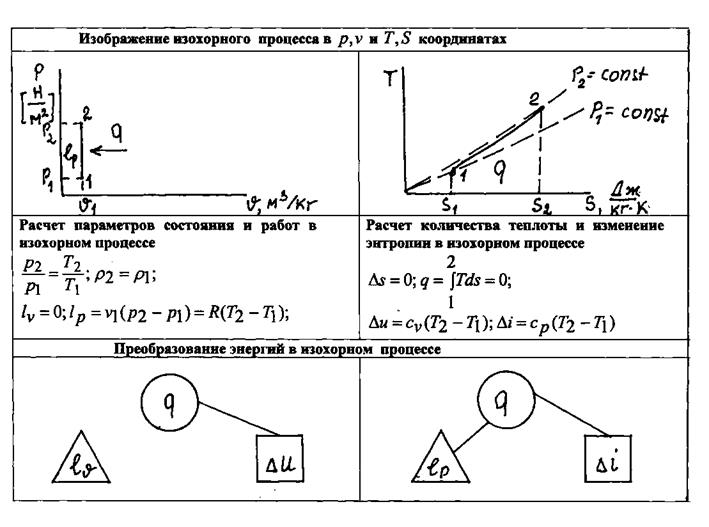
Рис.1.15. Изображение изохорного процесса в различных системах координат и преобразование энергий в этом процессе
1.14.5. Характеристики политропных процессов в зависимости от
значения показателя политропы.
На рис.1.16 и 1.17 показаны различные политропные процессы.
|
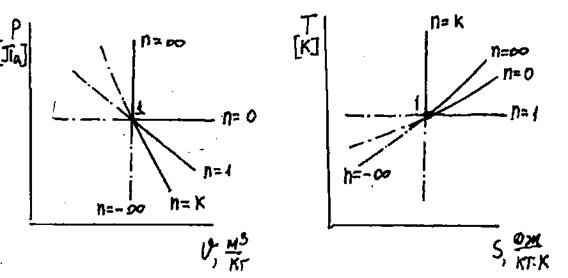
Рис.1.16. Изображение различных политропных процессов
в 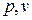 и
и 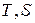 координатах
координатах
|
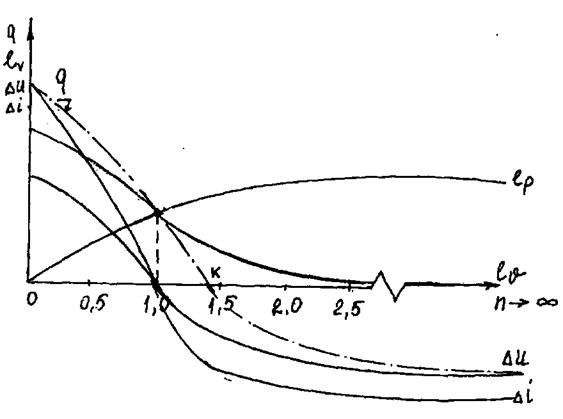
Рис.1.17. Энергии в различных политропных процессах.
Из этих рисунков видно, что существуют три диапазона значений показателя политропы:
1-я группа (0<п<1). Как показывает значение показателя, эти политропные процессы расположены между изобарой и изотермой и протекание их можно определить следующими характеристиками:
а) расширение газа; все процессы на этом участке проходят с повышением температуры и, следовательно, с увеличением внутренней энергии газа; объем газа увеличивается, т. е. газ расширяется и совершает деформационную работу. Таким образом, процесс проходит с подводом к газу теплоты, которая частично расходуется на нагрев газа и частично на работу расширения. По мере приближения значения показателя к единице часть теплоты, расходуемой на изменение внутренней энергии газа, приближается к нулю, температура уменьшается;
б) сжатие газа; вполне понятно, что все явления при сжатии газа проходят с обратным знаком. Объем газа уменьшается и на сжатие газа затрачивается работа; температура газа понижается и внутренняя энергия его уменьшается. Таким образом, от газа должна быть отведена теплота, полученная от убыли внутренней энергии и от работы, затраченной на сжатие газа.
Теплоемкость процессов меняется от 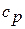 (при
(при 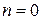 ) до
) до 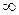 (при
(при 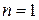 ). Значение коэффициента
). Значение коэффициента 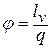 меняется от l/k (при
меняется от l/k (при 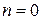 ) до 0 (при
) до 0 (при 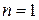 ).
).
2-я группа (1<n<k). Эти процессы располагаются между изотермой и адиабатой:
а) расширение газа; при изотермическом расширении работа получается за счет теплоты, подводимой извне; при адиабатном расширении работа совершается только за счет внутренней энергии газа. В процессах, расположенных между изотермой и адиабатой, работа газа совершается частично за счет теплоты, подведенной извне, частично за счет внутренней энергии газа; чем ближе значение п к единице, тем большая доля работы совершается за счет внешней теплоты; чем ближе значение п к значению k, тем большая доля работы совершается за счет убыли внутренней энергии газа, тем сильнее охлаждается газ;
б) сжатие газа; так как все явления проходят с обратным знаком, то в процессе сжатия частично увеличивается внутренняя энергия газа и теплота должна частично отводиться в окружающую среду; чем ближе значение п к единице, тем больше отводится теплоты в окружающую среду и тем меньше нагревается газ. В этих процессах теплоемкость имеет отрицательное значение и меняется от 0 до 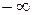 , что видно из уравнения
, что видно из уравнения 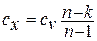 , где при n=k (адиабата)
, где при n=k (адиабата) 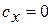 , а при
, а при 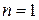
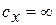 (изотерма).
(изотерма).
Отрицательное значение теплоемкости в этих процессах вполне объяснимо. Действительно, теплоемкость процесса определяет количество теплоты, которое необходимо подвести к газу в процессе для повышения его температуры на один градус; но нагрев можно осуществить не только подводом теплоты, но и в процессе сжатия газа.
В политропных процессах, расположенных между изотермой и адиабатой, при расширении газа работа совершается частично за счет внутренней энергии, и температура газа падает, но остальная, необходимая для работы теплота подводится из окружающей среды. Таким образом, при расширении, несмотря на подвод теплоты, газ охлаждается, что возможно только при отрицательном значении теплоемкости. Это видно из уравнения 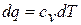 , где dq>Q, a dT<0.
, где dq>Q, a dT<0.
Такое же явление происходит и при сжатии газа; работа сжатия превращается в теплоту, но часть этой теплоты отводится в окружающую среду и только часть ее идет на нагрев газа. Следовательно, температура газа повышается при отводе теплоты и в приведенном уравнении 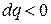 и
и 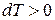 , что возможно только при отрицательном значении теплоемкости.
, что возможно только при отрицательном значении теплоемкости.
Значение величины 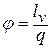 меняется от 0 при п=1 до оо при n=k.
меняется от 0 при п=1 до оо при n=k.
3-я группа (к<п< 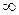 ). Эти процессы расположены между адиабатой и изохорой. Кривые процесса по мере увеличения значения п располагаются все более круто, приближаясь в пределе к прямой
). Эти процессы расположены между адиабатой и изохорой. Кривые процесса по мере увеличения значения п располагаются все более круто, приближаясь в пределе к прямой 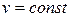 :
:
а) расширение газа; работа газа все время уменьшается, приближаясь к нулю (изохора); отводимое количество теплоты возрастает вследствие убыли внутренней энергии, и поэтому температура газа понижается быстрее;
б) сжатие газа; несмотря на то что работа сжатия газа уменьшается, температура его увеличивается по мере приближения значения п к 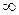 , так как количество теплоты, подводимое извне, все увеличивается; увеличение внутренней энергии газа происходит за счет суммарной теплоты, подводимой извне, и эквивалентной работы сжатия.
, так как количество теплоты, подводимое извне, все увеличивается; увеличение внутренней энергии газа происходит за счет суммарной теплоты, подводимой извне, и эквивалентной работы сжатия.
Теплоемкость в процессах по мере увеличения показателя политропы п от k до 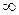 увеличивается от 0 до
увеличивается от 0 до 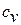 , что видно из уравнения
, что видно из уравнения 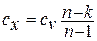 . Значение коэффициента
. Значение коэффициента 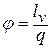 от
от 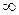 (при n=k) уменьшается до 1 (при
(при n=k) уменьшается до 1 (при 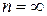 ). В этом можно убедиться, если уравнение
). В этом можно убедиться, если уравнение 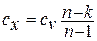 представить в следующем виде, полученном после деления числителя и знаменателя на п, причем при
представить в следующем виде, полученном после деления числителя и знаменателя на п, причем при  .
.
Из рис.1.17 можно сделать еще следующие выводы. Так как изотермы по мере удаления от начала координат характеризуют все более высокие температуры, то все процессы, идущие от начальной точки 1 вверх и вправо от изотермы, проходят с повышением температуры газа, то есть увеличением его внутренней энергии. Процессы, идущие от начальной точки 1 вниз и влево, проходят с понижением температуры газа и, следовательно, с уменьшением его внутренней энергии.
Таким образом, изотерма является границей процессов, проходящих с увеличением и уменьшением внутренней энергии газа.
Если рассматривать адиабату как границу процессов, то можно убедиться, что все процессы, проходящие вверх и вправо от адиабаты, идут с подводом теплоты, а идущие вниз и влево - с отводом теплоты в окружающую среду.
1.15. Уравнение сохранения энергии для потока газа.
Рассматривается открытая термодинамическая система – поток движущегося газа (рис.1.18). Рабочее тело с массовым расходом 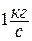 , перемещаясь от сечения «1-1» к сечению «2-2», характеризуется следующими видами изменения энергий:
, перемещаясь от сечения «1-1» к сечению «2-2», характеризуется следующими видами изменения энергий:
- внутренней энергии газа  ;
;
- кинетической энергии газа 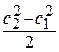 ;
;
- энергии положения относительно уровня моря 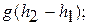

|
Рис.1.18. Поток газа
- энергии проталкивания газа 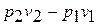
Все перечисленные изменения энергии были получены за счёт подвода потока извне теплоты 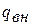 и внешней работы
и внешней работы 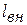 . Таким образом, получаем уравнение сохранения энергии в общем виде:
. Таким образом, получаем уравнение сохранения энергии в общем виде:
 (1.19)
(1.19)
При движении газа по каналу имеет место трение, на преодоление которого затрачивается работа 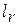 , которая эквивалентна количеству теплоты, подводимой к потоку из-за трения
, которая эквивалентна количеству теплоты, подводимой к потоку из-за трения 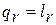 . Отсюда уравнение сохранения энергии с учётом трения записывается так:
. Отсюда уравнение сохранения энергии с учётом трения записывается так:
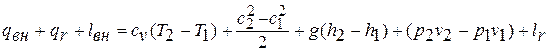
Сумма 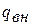 и
и 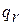 называется сообщенной теплотой потоку газа:
называется сообщенной теплотой потоку газа:
 .
.
Изменением энергии положения 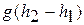 обычно пренебрегают ввиду малого отличия геометрических высот относительно уровня моря
обычно пренебрегают ввиду малого отличия геометрических высот относительно уровня моря 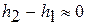 .
.
Изменение энергии проталкивания 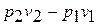 на основании уравнения состояния газа можно записать
на основании уравнения состояния газа можно записать 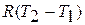 , а сумма
, а сумма 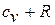 на основании уравнения Майера равна
на основании уравнения Майера равна 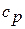 . В этом случае уравнение сохранения энергии имеет вид:
. В этом случае уравнение сохранения энергии имеет вид: 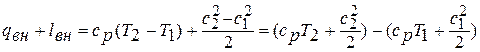
Сумма энтальпии 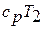 и кинетической энергии
и кинетической энергии 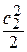 в сечении называется полной энергией или полной энтальпией
в сечении называется полной энергией или полной энтальпией 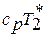 . Отсюда уравнение сохранения энергии можно трактовать так: подведенные извне теплота и работа расходуются на изменение полной энергии потока:
. Отсюда уравнение сохранения энергии можно трактовать так: подведенные извне теплота и работа расходуются на изменение полной энергии потока:
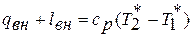
Для произвольного сечения потока выражение для полной энергии записывается в виде:  или
или 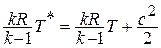
Разделим обе части уравнения на  :
: 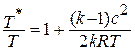
Из курса физики известно, что  равно квадрату скорости звука а2, а отношение скорости к скорости звука называется числом Маха
равно квадрату скорости звука а2, а отношение скорости к скорости звука называется числом Маха 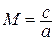 .
.
Данное отношение названо в честь Эрнста Маха (1838 – 1916), австрийского физика и философа; отношение является критерием( от греч. Kriterion – средство для суждения) – признаком, на основании которого производится оценка, определение или классификация чего - либо; мерило оценки; в данном случае критерий сжимаемости газа. Формула 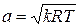 получается при допущении, что звуковая энергия (волна) распространяется в газе или жидкости в соответствии с уравнением адиабатного процесса
получается при допущении, что звуковая энергия (волна) распространяется в газе или жидкости в соответствии с уравнением адиабатного процесса 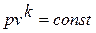 или
или 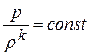 .
.
Дифференциальное уравнение этого процесса представляется так 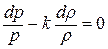 , или
, или 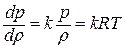 . Отношение
. Отношение 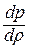 соответствует величине звуковой энергии (квадрату скорости распространения звука в веществе).
соответствует величине звуковой энергии (квадрату скорости распространения звука в веществе).
Отсюда выражение для полной энергии потока в сечении записывается так: 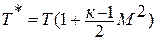
Число Маха, таким образом, является характеристикой сжимаемости рабочего тела. Например, при 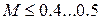 сжимаемостью газа можно пренебречь и принять
сжимаемостью газа можно пренебречь и принять 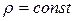 , то есть считать газ как жидкость. При
, то есть считать газ как жидкость. При 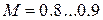 - околозвуковой поток, характерный для полетов гражданских самолетов; при
- околозвуковой поток, характерный для полетов гражданских самолетов; при 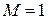 - звуковой барьер или критический режим течения потока; при
- звуковой барьер или критический режим течения потока; при  - трансзвуковой поток, характерный режим обтекания некоторых участков крыла самолета даже при околозвуковой скорости полета воздушного судна; при
- трансзвуковой поток, характерный режим обтекания некоторых участков крыла самолета даже при околозвуковой скорости полета воздушного судна; при 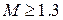 - сверхзвуковой поток; при
- сверхзвуковой поток; при 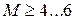 гиперзвуковой поток. Поскольку плотность воздуха в атмосфере Земли с высотой уменьшается практически до нуля, то число Маха в полете при этих условиях стремится к бесконечности (например, поток газа в пустоту).
гиперзвуковой поток. Поскольку плотность воздуха в атмосфере Земли с высотой уменьшается практически до нуля, то число Маха в полете при этих условиях стремится к бесконечности (например, поток газа в пустоту).
Принимая 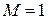 , находим критическую скорость звука, используя выражение:
, находим критическую скорость звука, используя выражение: 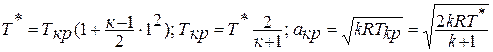
Если формулу для полной энергии потока разделить на  и обозначить отношение скорости к критической скорости звука как приведенную скорость
и обозначить отношение скорости к критической скорости звука как приведенную скорость 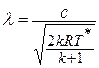 , то выражение для полной энергии потока в сечении (или для любой точки потока) представляется так
, то выражение для полной энергии потока в сечении (или для любой точки потока) представляется так
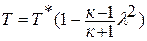 или
или 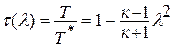 - газодинамическая функция температуры. Значение приведенной скорости меняется от нуля до максимального значения
- газодинамическая функция температуры. Значение приведенной скорости меняется от нуля до максимального значения 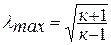 .
.
Если принять процесс торможения потока от температуры 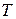 до
до 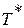 адиабатным, что практически соответствует приборам для измерения давления в потоке, то можно найти выражение для газодинамической функции давления
адиабатным, что практически соответствует приборам для измерения давления в потоке, то можно найти выражение для газодинамической функции давления 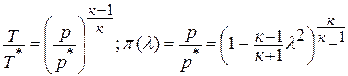
или плотности 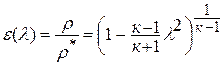 .
.
Уравнение сохранения энергии широко используется в авиационной практике для различных элементов двигателей. Например:
а) работа , подводимая к валу ротора компрессора 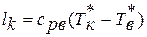 ;
;
Дата добавления: 2015-08-01; просмотров: 14135;
