Цикл Карно.

Циклом или круговым процессом тепловых машин называют совокупность термодинамических процессов, в результате совершения которых рабочее тело возвращается в исходное состояние.

В 1824 году французский физик и инженер Карно Никола Леонар Сади (1796 – 1832) впервыепредложил цикл тепловой машины, состоящий из двух адиабатических и двух изотермических процессов (рис.2.1, 2.2).

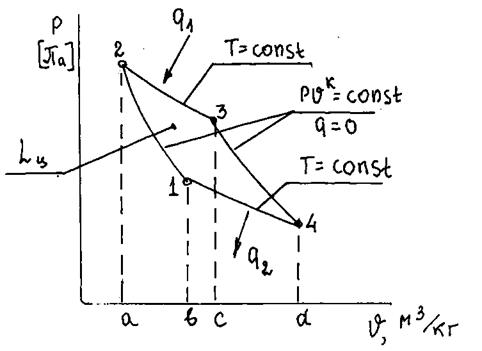
Рис.2.1. Изображение цикла Карно в 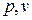координатах:

«1 – 2» - адиабатический процесс сжатия;

«2 – 3» - изотермический процесс расширения – подвод теплоты

к рабочему телу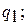

«3 – 4» - адиабатический процесс расширения;

«4 – 1» - изотермический процесс сжатия – отвод теплоты от

рабочего тела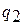

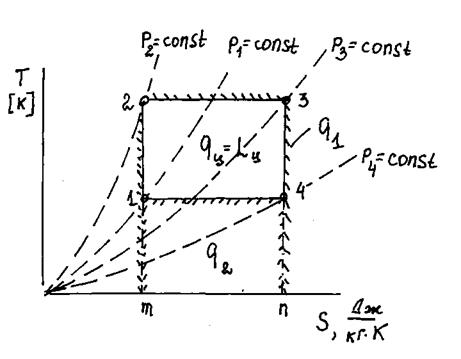
Рис.2.2. Изображение цикла Карно в 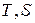координатах

Для расчёта цикла Карно принимаются следующие исходные данные:

- параметры состояния точки «1» (начало цикла): ;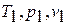

- степень сжатия в адиабатном процессе «1 – 2» ;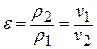

- удельное количество теплоты, подводимое к рабочему телу в изотермическом процессе «2 – 3»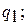

- показатель адиабаты и газовая постоянная рабочего тела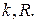

1.Расчет параметров состояния в контрольных точках цикла Карно производится в следующей последовательности:

Точка «2»: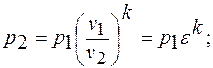

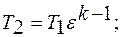
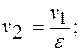
Точка «3»:

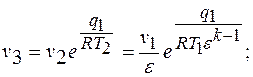
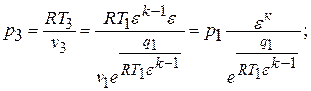
Точка «4»: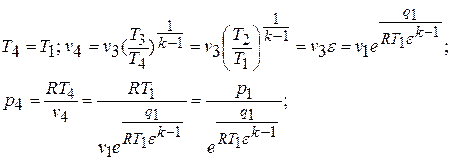

2.Далее производится расчёт энергий, участвующих в термодинамических процессах цикла Карно:

«1 – 2» - адиабатический процесс сжатия

- деформационная работа сжатия, эквивалентная площади фигуры 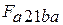на рис.2.1: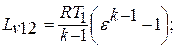

«2 – 3» - изотермический процесс расширения

- деформационная работа расширения, эквивалентная площади фигуры 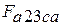на рис.2.1: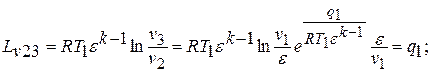

«3 – 4» - адиабатический процесс расширения

- деформационная работа расширения, эквивалентная площади фигуры 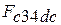на рис.2.1:

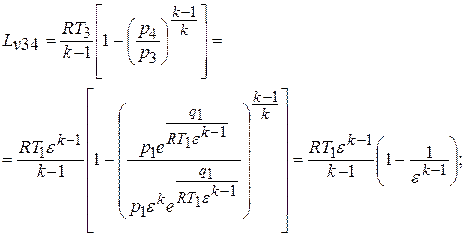
«4 – 1» - изотермический процесс сжатия

- деформационная работа сжатия, эквивалентная площади фигуры 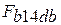на рис.2.1: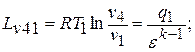

Работа цикла или свободная энергия на выходе из тепловой машины представляет собой алгебраическую сумму деформационных работ цикла

Карно или разность деформационных работ расширения и сжатия. На рис.2.1 работа цикла эквивалентна площади фигуры :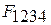

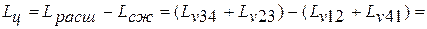
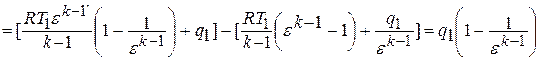
Эффективность цикла Карно оценивается по величине термического коэффициента полезного действия (КПД), определяемого отношением полезной работы цикла 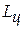к подведенной теплоте :

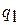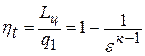
Рассмотрим теперь тепловую диаграмму 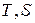(рис.2.2). Термический КПД цикла Карно можно представить так: ,

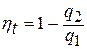где 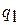- теплота, подведенная к рабочему телу в изотермическом процессе расширения «2 – 3» и эквивалентная площади фигуры 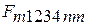на рис.2.2;

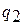- теплота, отведенная от рабочего тела в изотермическом процессе сжатия «4 – 1» и эквивалентная площади фигуры .

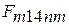В изотермических процессах теплота равна работе процесса, то есть

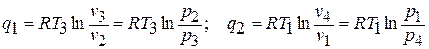
С другой стороны, для адиабатных процессов «1 – 2» и «3 – 4» справедливы зависимости: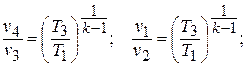

Отсюда 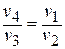или

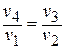
Полезно использованная теплота 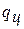в 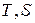диаграмме представляет собой разность подведенной и отведенной теплоты, то есть .

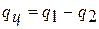На рис.2.2 эта теплота эквивалентна площади фигуры 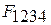, численно равна работе цикла и находится по формуле:

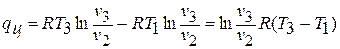
Термический КПД цикла равен отношению полезной теплоты к подведенной, то есть .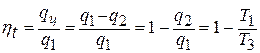

Из полученного выражения для термического КПД цикла Карно следует:

1) термический КПД определяется лишь интервалом температур,

в котором цикл осуществляется;

2) чем ближе значения 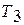и 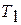, тем меньше термический КПД;

3) термический КПД не может быть равен единице, так как неосуществимо 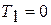ни , ни ;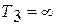

4) при отсутствии тел с разной температурой ( )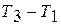

невозможно осуществить периодическое преобразование теплоты в работу;

5) любой произвольный цикл, осуществленный в том же интервале температур 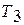и 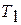, имеет меньший термический КПД, чем КПД цикла Карно.

Это означает, что работа произвольного цикла, эквивалентная площади фигуры 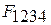, оказывается меньше таковой площади фигуры 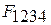для цикла Карно. Поэтому цикл Карно является базовым для всех произвольных циклов, а отношение термического КПД произвольного цикла к термическому КПД цикла Карно (в том же интервале температур) является показателем термодинамического совершенства произвольного цикла.

Приведенное обсуждение для термического КПД цикла Карно позволяет сформулировать второй закон термодинамики или второе начало термодинамики: