Деформационная работа всегда связана с перемещением макроскопических тел в пространстве, например, с перемещением поршня, деформацией оболочки,

поэтому она характеризует упорядоченную (макрофизическую) форму передачи энергии от од­ного тела к другому и является мерой переданной энергии.

Поскольку величина 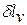пропорциональна увеличению объема, то в качестве рабочих тел, предназначенных для преобразования тепловой энергии в механическую работу, целесообразно выбирать такие вещества, которые обладают способностью значительно увеличивать свой объем. Этим качеством обладают газы и пары жидкостей. Поэтому, например, на тепловых электрических станциях рабочим телом служат пары воды, а в двигателях внутреннего сгорания — газообразные про­дукты сгорания того или иного топлива.

Аналогичные рассуждения можно привести и при анализе технической работы(рис.1.5). Здесь 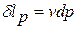- элементарная техническая работа, связанная с изменением давления на границах «рабочее тело – внешняя среда», характерная для открытой термодинамической системы.

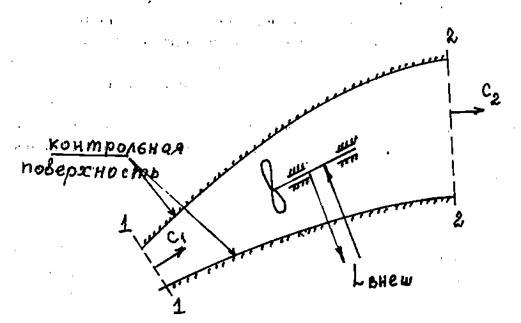
На рис.1.6 показан криволинейный канал, по которому движется газовый поток. Внутри канала размещается лопаточный аппарат, к которому может подводиться (например, для вращения вентилятора, компрессора, насоса и т.п.) или отводиться (например, при вращении турбины, тахометра и т.п.) внешняя механическая работа .

Рис.1.6. Пример открытой термодинамической системы – поток газа

в криволинейном канале:

1 – 1 – поперечное (контрольное) сечение газового потока на входе

в канал; 2 – 2 – то же на выходе из канала

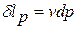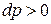В результате подвода этой энергии в рабочем теле либо возрастает давление (например, при сжатии газа), либо давление уменьшается (например, при расширении газа). То есть к рабочему телу может либо подводиться техническая работа при , либо отводиться при 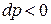. Для лопаточных аппаратов в данном случае техническая работа эквивалентна работе на окружности колеса турбомашины.

Интеграл 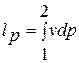в данном случае называют интегралом Д. Бернулли.

Поскольку при вычислении технической работы неизвестно изменение удельного объёма от давления 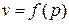, величина 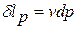не является полным дифференциалом. В 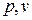диаграмме эта работа представляет собой площадь под кривой процесса «12» относительно оси давлений и крайними абсциссами.

1.6. Уравнение состояния для реального газа.

Для реального газа уравнение состояния впервые было разработано в 1873 году Йоханнесом Дидериком Ван-Дер-Ваальсом (1837 – 1923),нидерландским физиком (лауреатом Нобелевской премии в 1910 году):

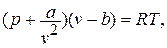(1.5)

где коэффициент «а» учитывает силы молекулярного притяжения каких либо частей газа; коэффициент «b» учитывает наименьший объём, до которого можно сжать газ.

Написанное уравнение оказывается 3 – ей степени относительно удельного объёма:

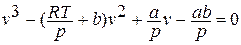
При различных значениях температуры Т приводит к следующим результатам.

1. В 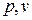диаграмме при высоких температурах изотермический процесс

реального газа ( 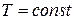) близок к изотермическому процессу идеального газа (линии «1 – 1^’» на рис.1.7). При этих условиях каждому значению давления отвечает определенная величина удельного объёма, то есть из трех корней уравнения только один корень действительный, а два других мнимые, иначе лишены физического смысла. Если температуру ещё более повысить, то новая изотерма «0 – 0^’» на рис.1.7 практически будет равнобокой гиперболой, как в случае идеального газа. Физически это связано с тем, что

при больших температурах влия­ние числа 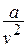, а затем и объёма молекул « 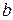» пренебрежимо мало.

2. Изотермы при низких температурах имеют вид, соответст­вующий кривой, например, «2—2'». Эта кривая пересекает линию 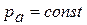в трех точках: a, b, c; следовательно, при низких температурах для каждого значения давления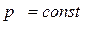

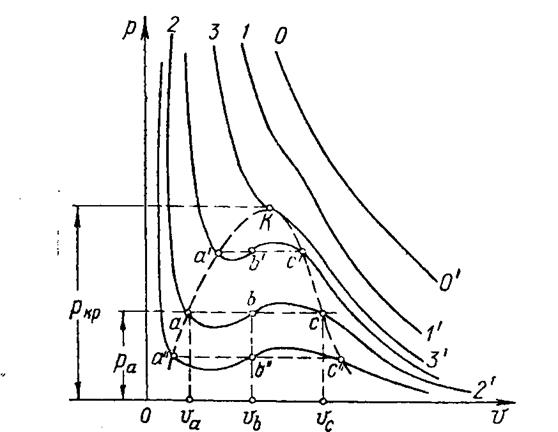
Рис.1.7. Изображение уравнения состояния реального газа в

диаграмме

уравнение состояния Ван-Дер-Ваальса даёт три действительных корня: .

На графике рис.1.7 нанесены три такие изотермы. Для изотермы «2—2'» участок кривой «2 – а» соответствует жидкой фазе вещества; точка «а» начало кипения. Точка «с» соответствует полному испарению жидкости, при этом пар находится при температуре кипения, соответствующей давлению: в точке «b» - двухфазная среда (жидкость и пар). Следовательно, волнообразный участок a – b – c изотермы «2—2'» по уравнению Ван-Дер-Ваальса соответствует процессу испарения жидкости, что противоречит опыту: на этом остановимся несколько ниже. Чем выше температура в этой области, тем короче участок волнообразной кривой.

3. Наконец, для каждого вещества есть своя единственная изотерма

«3 – 3^’», кривая которой в некоторой точке «к» имеет перегиб. Для этой изотермы все три корня уравнения Ван-Дер-Ваальса получают действительные и равные значения. Верхний участок «3 – к» кривой «3 – 3^’» соответствует границе двухфазного (жидкого и газообразного) состояния вещества; нижний участок k—3' соответствует парообразному и в правой части при низких давлениях газообразному состоянию. Таким образом, по изотерме «3 – 3^’» нет такого процесса испарения, который был, например, по изотер­ме «2—2'». Вещество в точке «к» может находиться и в жидком, и в газообразном состояниях. Ничтожно малое увеличение темпе­ратуры (или давления при ) сразу переводит жидкость в пар; наоборот, незначительное уменьшение температуры пере­водит пар в жидкость. Точка «к» называется критической, а тем­пература, давление и удельный объем в этом состоянии называ­ются соответственно критической температурой 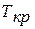, критическим давлением 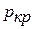и критическим удельным объемом .

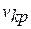Если давление 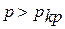, температура 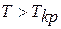, то невозможен переход пара в жидкость; вещество может находиться только в однофазном состоянии (пар, газ).

В таблице 1.3 приводятся зна­чения критических параметров состояния некоторых веществ.

Таблица 1.3