Визначення втрат енергії при ламінарному режимі течії рідини в трубі круглого поперечного перерізу

Математично можна довести, що епюра швидкостей в поперечному перерізі труби при ламінарній течії рідини є квадратичною параболою, рівняння якої згідно з рис.3.7 має вигляд:

.

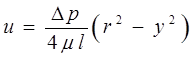(3.24)

В цьому рівнянні: 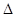р=p₁–p₂ – втрати тиску між двома даними перерізами труби; l – відстань між двома перерізами; r – радіус труби;
у – відстань від осі потоку (труби), змінюється від 0 до r ; 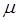– динамічний коефіцієнт в’язкості.

Рис.3.7

Очевидно, що максимальна швидкість потоку буде при у=0, тобто на осі труби; величина її визначається формулою:

.

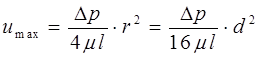(3.25)

де d – діаметр труби.

Середня швидкість рідини виявляється вдвічі меншою за максимальну:

.

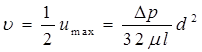(3.26)

Втрати напору (енергії) на тертя знаходяться за формулою Пуайзеля, яка виходить зі співвідношення (3.26):

.

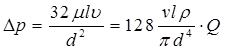(3.27)

В останньому рівнянні 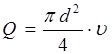– об’ємна витрата рідини;
ν – кінематичний коефіцієнт в’язкості; ρ – густина рідини.

Якщо гідравлічні втрати виразити не в одиницях тиску, а в лінійній розмірності, то отримаємо такі залежності:

,

(3.28)

або

.

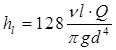(3.29)

Закон Пуайзеля можна привести до вигляду формули Дарсі-Вейсбаха (3.18). Для цього помножимо і поділимо праву частину рівняння (3.27) на середню швидкість υ. Після деяких перетворень кінцево отримаємо:

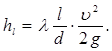
Прирівняємо втрати напору по довжині, визначенні за формулами (3.19) і (3.29):

.

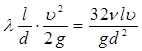Звідсіля гідравлічний коефіцієнт тертя при ламінарному режимі

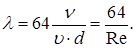
(3.30)

В загальному випадку ламінарної течії:

.

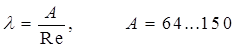(3.31)

Місцеві опори в трубопроводах при ламінарному режимі течії рідини значно менші порівняно з опором сил гідравлічного тертя; до того ж закономірності їх зміни мало досліджені. Тому місцеві опори враховують як частку лінійних втрат через еквівалентну довжину трубопроводу.