Рівняння Бернуллі для елементарної струминки і потоку в’язкої рідини

На відміну від ідеальної рідини при русі в’язкої(реальної) рідини частина енергії, яку вона має, витрачається на подолання сил опору (внутр. тертя, вихроутвор. та ін.). Отже питома енергія в будь-якому наступному в напрямі течії поперечному перерізі буде меншою порівняно з питомою енергією в попередньому перерізі. Тому рівняння Бернуллі для елементарної струминки реальної рідини буде мати вигляд

.

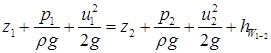(3.13)

де 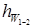– втрати енергії (напору) струминки між обраними перерізами.

Рівняння Бернуллі для потоку реальної рідини отримують інтегруванням рівняння (3.13) з заміною дійсних швидкостей окремих струминок, що утворюють потік, на середню швидкість υ рідини в даному перерізі (рис.3.6):

.

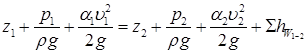(3.14)

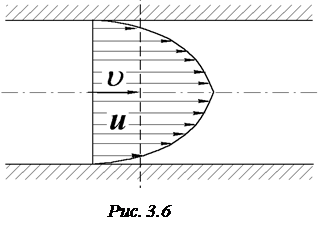
Коефіцієнт α, що входить до рівняння Бернуллі, називають коефіцієнтом кінематичної енергії або коефіцієнтом Коріоліса. Він враховує нерівномірність розподілу швидкостей в перерізі потоку і фактично є відношенням дійсної кінетичної енергії потоку в даному живому перерізі до кінетичної енергії, обчисленої за середньою швидкістю потоку. Величина коефіцієнта α в залежності від характеру течії рідини змінюється в межах від 1,04…1,12 до 2. Складова рівняння 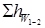– це сумарні втрати питомої енергії (напору) потоку між обраними перерізами.

Запишемо рівняння Бернуллі (3.14) в такій формі:

,

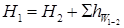(3.14’)

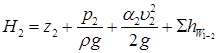де і – повні гідродинамічні напори потоку в перерізах 1–1 та 2–2 відповідно.

Відношення втрат напору до довжини ділянки потоку, обмеженої перерізами 1–1 і 2–2, називають гідравлічним уклоном, або градієнтом втрат напору:

,

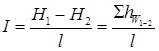(3.15)

тут l – довжина ділянки, м.