Рівняння Бернуллі при усталеному русі ідеальної рідини

Розглянемо усталений рух ідеальної рідини, яка знаходиться під впливом тільки масової сили – сили ваги, - і отримаємо для цього випадку рівняння, що зв’язує між собою тиск в рідині і швидкість її руху.

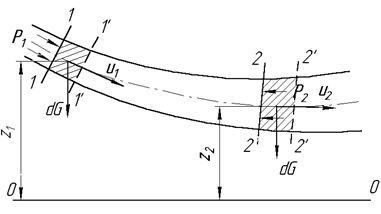
Рис.3.4

Візьмемо одну з елементарних струминок потоку ідеальної рідини і виділимо на ній ділянку довільної довжини, обмежену перерізами 1–1 і 2–2 (рис.3.4). Позначимо через dω₁, p₁, u₁, z₁ і dω₂, p₂, u₂, z₂ відповідно площі живих перерізів, гідродинамічні тиски, швидкості рідини і висоти центрів ваги даних перерізів над площиною порівняння 0–0.

За нескінченно малий проміжок часу dt відсік 1–2 переміститься в положення .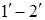

Застосуємо до виділеного відсіку теорему механіки про зміну кінетичної енергії, згідно з якою приріст кінетичної енергії відсіку за певний проміжок часу дорівнює сумі робіт всіх сил, що діють на відсік за цей же проміжок часу. Оскільки рідина ідеальна, то роботу будуть виконувати сили тиску і сили тяжіння.

Робота сил тиску буде дорівнювати:

.

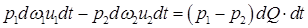Робота сил ваги:

.

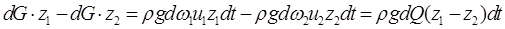Приріст кінетичної енергії відсіку 1–2 за час dt дорівнює різниці кінетичних енергій ділянок струминки 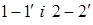(ділянка 1-2’ не змінює свого положення):

,

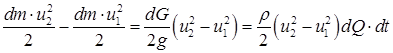(при перетвореннях враховано, що ; )/

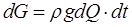Тоді теорема про зміну кінетичної енергії відсіку струминки буде мати вигляд:

.

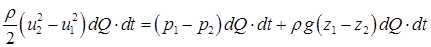(3.10)

Поділимо попереднє рівняння на dQdt і після перегрупування складових його отримаємо

.

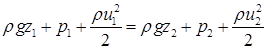(3.11)

Якщо поділити рівняння (3.13) на комплекс 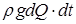, то після перегрупування складових будемо мати

.

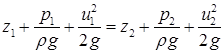(3.12)

Останні два рівняння і є рівнянням Бернуллі для елементарної струминки ідеальної рідини в двох різних формах. Так, всі складові в рівнянні (3.11) мають розмірність тиску, а складові рівняння (3.12) – лінійну розмірність.

З’ясуємо геометричну і фізичну суть рівняння Бернуллі/

Геометрична інтерпретація рівняння:

z – геометрична висота, або геометричний напір;

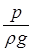– п’єзометрична висота, або п’єзометричний напір;

– швидкісна висота, або швидкісний напір.

Тричлен 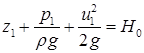називають повним, або гідродинамічним напором. Оскільки рівняння Бернуллі записане для довільних перерізів струминки, то H₀=const в будь-якому перерізі цієї струминки (рис.3.5).

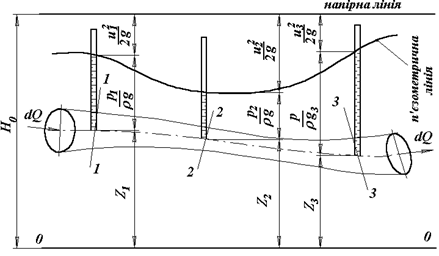
Рис.3.5

З енергетичної точки зору рівняння Бернуллі є законом збереження питомої енергії ідеальної рідини. Дійсно, якщо рівняння (3.11) записати у вигляді

,

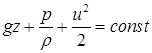то 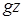– питома енергія положення, Дж/кг;

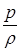– питома енергія тиску, Дж/кг;

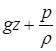– питома потенціальна енергія рідини, Дж/кг;

– кінетична енергія віднесена до одиниці маси, Дж/кг.

Можна теоретично довести, що для потоку ідеальної рідини з повільно-змінним рухом сума z+p/ρg для всіх точок живого перерізу є постійною. Крім того, в даному живому перерізі потоку ідеальної рідини швидкості всіх елементарних струминок однакові. Тому рівняння Бернуллі для потоку ідеальної рідини має такий же вигляд як і для елементарної струминки, тобто дається формулами (3.11) і (3.12).