Сила тиску рідини на криволінійні поверхні

Визначення сили сумарного тиску рідини на поверхні довільної форми в загальному випадку зводиться до визначення трьох складових цієї сили і трьох моментів /в системі координат Оху/

В техніці переважно мають справу з циліндричними або сферичними поверхнями, які мають вертикальну площину симетрії.

Розглянемо посудину з боковою стінкою циліндричної форми, котра заповнена рідиною, на вільну поверхню якої діє тиск р₀ і визначимо силу тиску на ділянку АВ цієї стінки в двох випадках:

1) рідина знаходиться над стінкою (рис.2.7а);

2) рідина знаходиться під стінкою. (рис.2.7б).

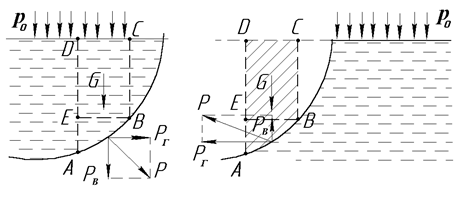
a), б)

Рис.2.7

В першому випадку виділимо об’єм АВСD рідини, обмежений ділянкою АВ стінки, вертикальними поверхнями АD і ВС, що проведені через границі цієї ділянки, і вільною поверхнею рідини. Сумарну силу тиску Р на ділянку АВ розкладемо на дві складові: вертикальну Р_В і горизонтальну Р_Г. З умови рівноваги об’єму АВСD у вертикальному напрямі знаходимо що

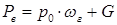,	(2.21)

Де G- вага виділеного об’єму рідини; ω_Г – площа проекції поверхні АВ на горизонталь.

В свою чергу сила ваги 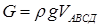. Об’єм рідини, що міститься в геометричній фігурі АВСD часто називають “тілом тиску” і позначають через V_тт. З урахуванням цього рівняння (2.21) запишеться у формі

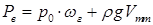.	(2.22)

При визначенні горизонтальної складової сили тиску на поверхню АВ потрібно урахувати, що сили тиску на поверхні ВС і DЕ взаємно зрівноважуються. Тоді

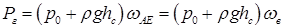.	(2.23)

В останньому рівнянні h_c – заглиблення центра ваги (мас) вертикальної проекції поверхні АВ – ω_в

Очевидно, що повна сила тиску на циліндричну поверхню

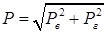.	(2.23)

Коли рідина розташована під стінкою рис.2.7б складові Р_в і Р_г також визначаються формулами 2.21 або 2.22 і 2.23 , але мають протилежний напрям. При цьому під силою ваги G розуміють вагу рідини в об’ємі АВСD, хоча останній не заповнений рідиною; тіло тиску V_ТТ є фіктивним.

Слід відмітити, що в тих випадках, коли циліндрична поверхня є коловою, лінія дії рівнодіючої сил тиску напрямлена по радіусу.