Основне рівняння гідростатики

Розглянемо найбільш поширений випадок рівноваги рідини, коли вона знаходиться тільки під дією сили тяжіння. Тоді проекції одиничних масових сил на координатні осі будуть такими: Х=0, Y=0, Z=-g (координатну вісь Oz вважаємо напрямленою вверх), і рівняння поверхні рівного тиску (2.7) набуває вигляду:

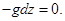
Звідкіля

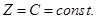
(2.8)

Таким чином, при рівновазі рідини в полі сил тяжіння поверхні рівня являють собою сім’ю горизонтальних площин. Однією з поверхонь рівного тиску буде і вільна поверхня рідини.

Визначимо тиск в довільній точці А об’єму рідини, що міститься в закритій посудині (рис.2.4) і знаходиться у стані спокою.

При X=0, Y=0, Z=-g основне диференціальне рівняння гідростатики (2.6) запишеться так:

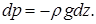
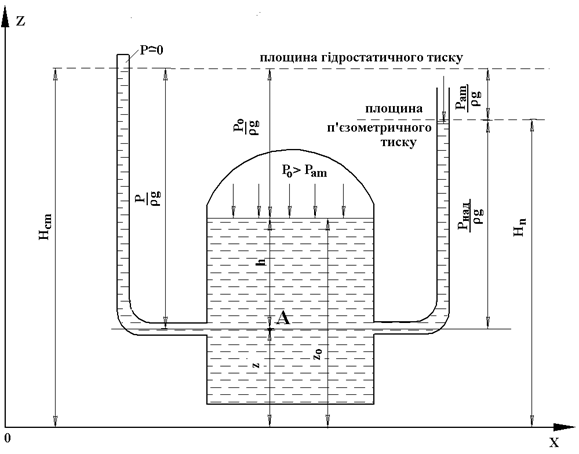
Рис.2.4

Після інтегрування в припущенні r=const отримаємо:

,

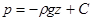(2.9)

де С-стала інтегрування.

Сталу інтегрування визначимо з граничних умов на вільній поверхні рідині в посудині, де z=z₀, p=p₀. Маємо:

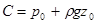і тоді ,

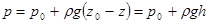(2.10)

де h=z-z₀ – заглиблення точки А під вільну поверхню.

Це і є основне рівняння гідростатики, яке виражає залежність тиску в даній точці рідини в стані спокою від виду рідини і відстані точці від вільної поверхні.

В рівнянні (2.10) р - абсолютний тиск в даній точці рідини, р₀ - зовнішній абсолютний тиск на вільній поверхні рідини; 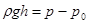- тиск стовпа рідини в даній точці. Всі складові рівняння мають розмірність тиску (ПА, кПА, МПА).

Основному рівнянню гідростатики можна надати іншого вигляду, якщо поділити всі його члени на ρg:

(2.11)

В цьому рівнянні складові мають лінійну розмірність (М).

Зв’язок між тиском, виражений в одиницях тиску (ПА), і тиском в лінійних одиницях (метрах стовпа рідини) дає загальна формула

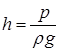
(2.12)

У відкритих резервуарах, водоймищах тощо зовнішнім тиском на вільну поверхню рідини є атмосферний тиск (р_ат,, р_бар). В таких випадках рівняння (2.10) записують у формі

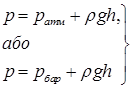
(2.13)

В техніці часто зустрічаються випадки, коли абсолютний тиск в даній точці рідини 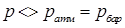. Тоді величину 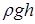називають надлишковим тиском:

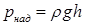
Якщо , то надлишковий тиск називають манометричним тиском:

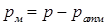
(2.14)

якщо 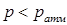то надлишковий тиск буде від’ємним і величину - називають вакууметричним тиском або вакуумом:

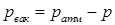
(2.15)

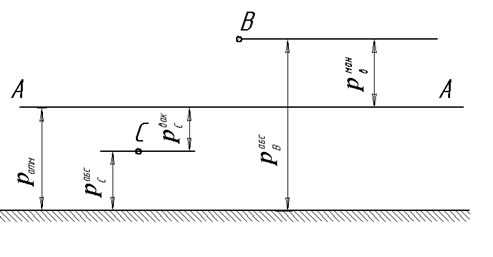
Рис.2.5

Зв’язок між абсолютним, манометричним і вакуумометричним тиском графічно проілюстрований на рис.2.5.

Гідростатичний закон розподілу тиску, виражений формулою (2.11), cправедливий для будь-якого положення координатної площини хОу. Цю площину називають площиною порівняння. Величина 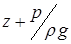, где z – геометрична висота розташування точки над площиною порівняння, р – абсолютний тиск, називається гідростатичним напором і позначається через 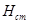; величину 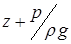, в якій р – надлишковий тиск, називають п’єзомеричним напором і позначають через 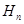. Як виходить з формули (2.11) напори 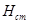і 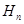є сталими для всіх точок даної маси рідини, що знаходиться в стані спокою.