Диференціальні рівняння рівноваги рідини

Виділимо в нерухомій рідині нескінченно малий об’єм у вигляді паралелепіпеда з ребрами dx, dy, dz (рис 2.3). Подумки відкинемо рідину, що оточує паралелепіпед, і замінимо її дію відповідними силами. Припустимо, що на ліву грань діє тиск р. Тоді на праву грань А₁В₁С₁D₁, яка знаходиться на відстанні x+dx, буде діяти тиск .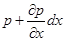

Відповідно, сила тиску на ліву грань АВСD буде дорівнювати

,

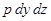а на праву

(

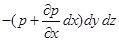
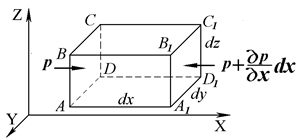
Рис.2.3

Знак (-) показує, що сила діє у від’ємному напрямі осі х)

Крім сили тиску на паралелепіпед може діяти рівнодіюча масових сил (тяжіння, відцентрова, інерції), проекція якої на вісь х буде:

,

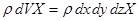де Х-проекція прискорення (одиничної масової сили) на вісь х;

dV-об’єм паралелепіпеда.

Рівняння рівноваги сил, що діють на паралелепіпед в напрямі осі х, має вигляд:

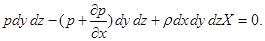
чи, після спрощень,

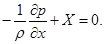
Аналогічно можна отримати рівняння рівноваги сил відносно осей y і z

Таким чином, кінцево маємо систему:

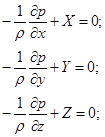
(2.5)

Рівняння (2.5) є основними диференціальними рівняннями рівноваги рідини (рівняння Ейлера).

Щоб привести рівняння Ейлера до вигляду, зручного для інтегрування, помножимо кожне з рівнянь (2.5) відповідно на dx, dy, dz і складемо їх почленно:

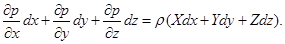
Ліва частина цього рівняння є повним диференціалом тиску dp, тому:

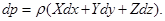
(2.6)

Рівняння (2.6) називається основним диференціальним рівнянням гідростатики.

Зі співвідношення (2.6) можна отримати рівняння для поверхні рівного тиску (поверхні рівня). Для такої поверхні p=const і при r=const будемо мати:

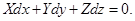
(2.7)

Частинним випадком поверхні рівня є вільна поверхня рідини.

Поверхні рівня мають такі властивості:

1) дві різні поверхні рівня не можуть перерізати одна одну;

2) зовнішні об’ємні сили напрямленні по нормалі до поверхні рівня.