Сила тиску рідини на плоску стінку. Центр тиску

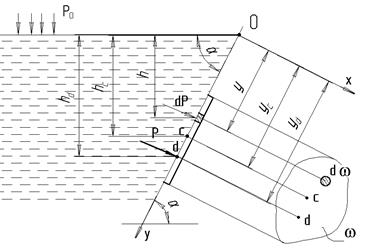
Визначимо силу тиску рідини на площину ω плоскої стінки, яка розташована під довільним кутом 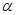до горизонту. Розв’язання задачі зручно проводити в системі координат хОу, вісь Оу якої напрямлена вздовж стінки, а вісь Ох співпадає з лінією перетину стінки і вільної поверхні рідини. Для зручності вісь Ох повернута на кут 90⁰, (рис.2.6).

Очевидно що між будь – якою координатою у і глибиною занурення h існує зв’язок: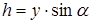

Сила тиску dР на довільну елементарну площину dω

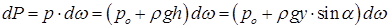
де р_о – тиск на вільній поверхні рідини густиною ρ.

Повна сила тиску на площину w стінки:

^*)

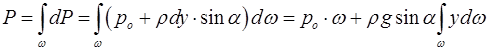
Рис. 2.6

Для зручності вісь Ох повернута на кут 90^о

Інтеграл 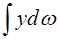є статичним моментом площини W відносно осі Ох, величина якого дорівнює добутку ω на відстань її центра ваги до осі Ох тобто

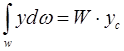
Тоді

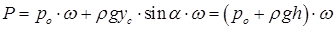
(2.16)

де h_с – глибина занурення центра ваги стінки площиною ω. Сила тиску самої рідини без урахування зовнішнього тиску p.

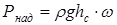
(2.17)

У випадку, коли плоска стінка горизонтальна і розміщена на глибині h ,то h_c=h і

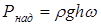
(2.18)

Якщо плоска стінка вертикальна α=90^о і h_c=y_c.

Досить часто в інженерних розрахунках важливо не тільки визначити величину сили тиску рідини, але й знайти точку прикладення її рівнодіючої – так званий центр тиску.

Для цього користуться теоремою Варіньйона: момент рівнодіючої сили дорівнює алгебраїчній сумі моментів сладових її. Відповідно до рис.2,6 можна записати

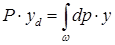
де у_d – координата центра тиску , Р=Р_над – сила тиску рідини.

Тоді

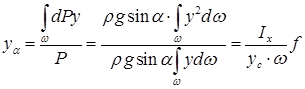
(2.19)

Тут – момент інерції змоченої площини ω відносно осі Ох ; у_сω – статичний момент цієї площини.

На підставі теореми про моменти інерції відносно паралельних осей /теорема Гюйгенса/

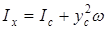
де I_c – момент інерції плоскої фігури відносно осі, що проходить через її центр ваги паралельно осі Ох, тому залежності (2.19) можна надати вигляду

.

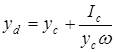(2.20)