Диференціальне рівняння Нав’є – Стокса

При русі реальної (в’язкої) рідини в потоці діють сили: масові, гідростатичного тиску, тертя, а також сили стиску й розтягування. Нав’є і Стоксом виведена система диференціальних рівнянь руху реальної рідини має вигляд (2.22), у якій:

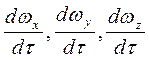– проекції зовнішніх сил на відповідні осі систем

координат;

X,Y,Z – проекції на відповідні осі масових сил, віднесених

до одиниці маси;

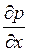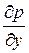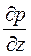, , - проекції гідростатичного стиску, діючого уздовж осей.

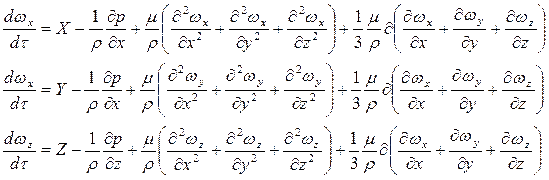, (2.22)

- сума других похідних по осі х має назву оператор Лапласа.

Отже, проекції рівноважної сил тертя на вісь х має вигляд

.

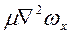Аналогічно для осей у, z.

При русі рідини, що стискається, у ній додатково виникають спричинені тертям сили стиску і розтягування, рівняння Нав’є-Стокса набувають вигляду:

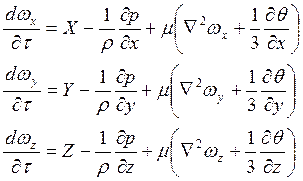, (2.23)

де часткові похідні 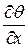, , 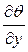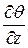виражають зміни швидкостей по осях x, y, z, пов’язані з дією сил стиску і розтягування, причому

.

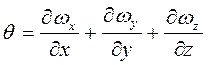Повне описання руху в’язкої рідини в його найбільш загальній формі можна отримати шляхом вирішення системи рівнянь Нав’є-Стокса разом з рівнянням нерозривності потоку (2.20, 2.21). Однак ці рівняння не можуть бути вирішені в загальному вигляді. Вирішують їх при низці спрощуючих припущень або при перетворенні цих рівнянь за допомогою методів теорії подібності.