Диференціальні рівняння руху Ейлера
В різних точках рідини, що рухається, в результаті дії зовнішніх сил виникає тиск, який називають гідродинамічним. Припустимо, що на рідину, яка рухається, діють об’ємні сили, проекції яких на осі координат, віднесені до одиниці маси, відповідно дорівнюють X, Y, Z. Сили тиску й масові сили, які входять в диференціальне рівняння рівноваги, представлені у вигляді проекцій на координатні осі x, y, z. причому, ці проекції віднесені до одиниці маси. Тому і проекції сил інерції потрібно приєднати до рівнянь рівноваги віднесеними до одиниці маси, тобто у вигляді:
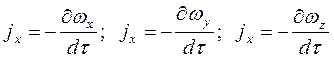 .
.
Знак мінус показує, що сили інерції направлені у бік, протилежний прискоренню.
З системи диференціальних рівнянь (2.23) з урахуванням дії масових сил, а також припускаючи, що рідина ідеальна, тобто
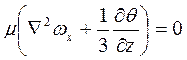
маємо систему диференційних рівнянь Ейлера:
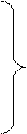
 . (2.24)
. (2.24)
Отримана система рівнянь (2.24) встановлює зв’язок між проекціями об’ємних сил і швидкостей, тиском і густиною рідини.
Субстанціанальні похідні відповідних складових швидкості дорівнюють:
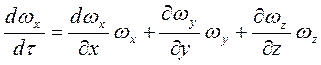 , (2.25)
, (2.25)
аналогічно для 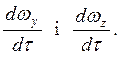
Для несталого потоку:
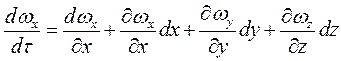 , (2.26)
, (2.26)
аналогічні рівняння для 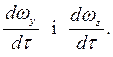
Дата добавления: 2015-08-26; просмотров: 834;
