Рівномірний рух рідини

Розглянемо рух рідини у нахиленому трубопроводі.

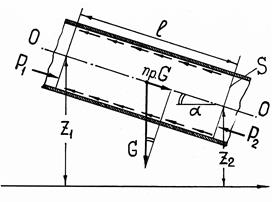
Виділяємо у трубопроводі відрізок довжиною l (рис. 22а).

б
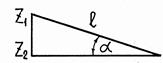
Рис. 22. До виведення рівняння руху рідини в нахиленому трубопроводі:   а – ділянка трубопроводуз позначеннями; б – трикутник розташування центрів тяжіння перерізів
а

Поміщаємо даний відрізок у систему координат. При рівномірному русі рідини у ній діють сили:

- масові G=rgV;

- гідростатичного тиску p₁S і p₂S;

- внутрішнього тертя F_тер=t₀S₀.

де S – поперечний переріз потоку;

S₀=lП – площа тертя на відрізку труби довжиною l ;

П – периметр трубопроводу;

t₀ – дотична напруга сили тертя.

Оскільки рух рівномірний, то сума проекцій усіх сил на будь-яку вісь дорівнює нулю. Розглянемо проекцію сил на вісь трубопроводу. Складемо рівняння балансу сил:

Gsina + p₁S - p₂S - t₀Пl = 0.(2.31)

З трикутника (рис.22 б)

z₁- z₂= l sin a.(2.32)

Виконуючи подальші перетворення, отримуємо рівняння:

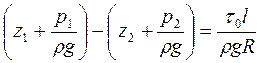. (2.33)

З рівняння (2.33) отримаємо гідравлічний нахил

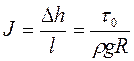, (2.34)

де R – гідравлічний радіус.

Гідравлічний нахил можна розглядати як втрати питомої енергії потоку, віднесені до одиниці довжини потоку.

З (2.34) отримаємо рівняння рівномірного руху рідини

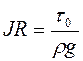. (2.35)

Це рівняння показує, що напруга сили тертя, віднесена до одиниці ваги рідини, дорівнює добутку гідравлічного нахилу на гідравлічний радіус.