Розподіл швидкості по горизонтальному перерізу труби

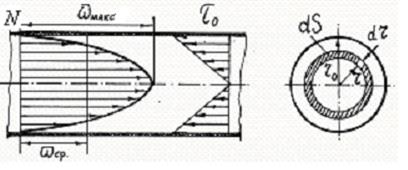
Розглянемо ламінарний рух рідини у трубопроводі (рис. 23а), в якому: r₀ – повний радіус, r – поточний радіус, t – дотична напруга, v – вектор швидкості, N – вектор підрахунку, який починається від стінки трубопроводу.

Виділимо з рівняння рівномірного руху (2.35) дотичну напругу

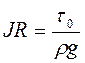® t₀ = rgJR.

Рис. 23. До виведення рівняння розподілу швидкості рідини по горизонтальному перерізу труби.

і з рівняння Ньютона для в’язкої рідини (1.24)

® .

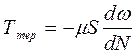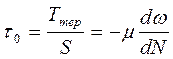Прирівнявши праві частини цих рівнянь і замінивши dN на dr, отримаємо

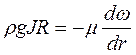.(2.36)

Оскільки для труби круглого перерізу гідравлічний радіус R =r/2, (2.36) можна записати у вигляді:

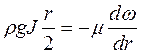. (2.37)

Поділимо перемінні інтегрування й запишемо диференціальне рівняння:

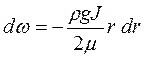, (2.38)

і, проінтегрувавши по радіусу і швидкості, отримаємо:

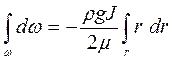, звідки 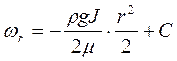. (2.39)

Для визначення сталої інтегрування С необхідно, щоб функція швидкості дорівнювала нулю. При цьому r=r₀.

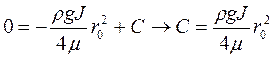. (2.40)

Підставивши (2.40) у (2.39), отримаємо формулу швидкості при ламінарному русі рідини:

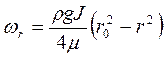. (2.41)

При r=r₀, тобто у центрі потоку, швидкість набуває максимального значення

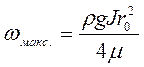. (2.42)

Якщо порівняти вираження 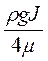з (2.41) і (2.42), то отримаємо

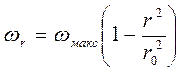. (2.43)

(2.43) – математичне вираження закону Стокса, який характеризує розподіл швидкостей у перерізі трубопроводу при ламінарному русі.