Турбулентний рух

При турбулентному режимі руху на відміну від ламінарного характер потоку порушується. Всі цівки перемішуються, траєкторії рухомих частинок набувають вельми складної форми.

Чисельні експерименти, проведені І. Нікурадзе, Г.Г. Гуржієнком та ін. показують, що при турбулентному режимі руху вектор швидкості в кожній точці потоку змінюється як за величиною, так і за напрямом, тобто пульсує. Однак, якщо вимірювати якусь складову цього вектора в точці протягом певного часу Т, то її значення практичне постійне (рис. 24). Така швидкість називається осередненою. Вона визначається залежністю

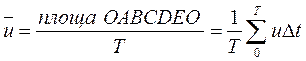, (2-51)

де Т – час осереднення.

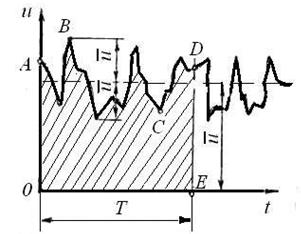
Рис. 24. Пульсація складової вектора швидкості у точці потоку при турбулентному русі.

Різниця між миттєвим значенням складової швидкості и і її осередненим значенням 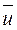називається пульсаційною добавкою і позначається и^`:

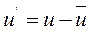. (2-52)

Розподіл швидкостей в трубопроводі при турбу­лентному режимі (рис. 25) можна описати формулою

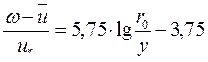, (2-53)

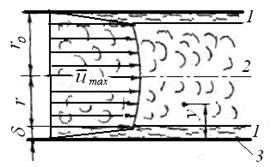
Рис. 25. Розподіл швидкостей в трубопроводі при турбулентному режимі руху:

1 - ламінарна плівка; 2 - турбулент­не ядро; 3 - стінка трубопроводу.

де ω =Q/S – середня швидкість руху рідини в трубі; 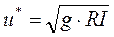– динамічна швидкість, або швидкість до­тичного напруження (це та швидкість, яку мала б рідина біля стінки при відсутності напруження тертя на стінці); у – відстань від стінки труби до точки, в якій визнача­ється швидкість 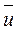; R – гідравлічний радіус; I – гідравлічний уклін.

Для формування в трубопроводі при турбулентному режимі руху відповідної йому епюри швидкостей необхід­на довжина початкової ділянки від входу в трубопровід визначається формулою

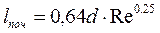. (2-54)

Закони турбулентногоруху рідини досліджувалися вченими Прандтлем, Нікурадзе та ін. Встановлено, що при русі рідини біля твердих тіл на поверхні останніх утворюється тонка плівка рідини. Рух рідини в межах цієї плівки завжди ламінарний, незважаючи на те, що в основному потоці (у ядрі течії) рух має турбулентний характер. Товщина ламінарної плівки дуже мала і залежить від швидкості, в’язкості рідини та розмірів потоку. Товщину ламінарної плівки можна підрахувати за одним із рівнянь

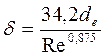, (2.55)

або

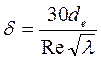. (2.56)

При використанні рівняння (2.56) спочатку коефіцієнтом тертя задаються (в межах від 0,05 до 0,02) а потім його значення уточнюють.

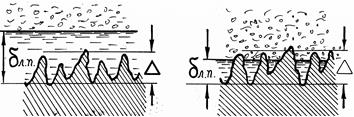
Значення коефіцієнта тертя залежить від абсолютної шорсткості стінки, тобто середньої висоти виступів Δ або e і товщини ламінарної плівки δ (див. рис.26 а і б).

а б

Рис. 26. Висота виступів на стінках труби і товщина ламінарної плівки: а – гідравлічно гладка труба; б – “шорстка” труба

Якщо δ>e, труба розглядається як “гідравлічно гладка” (рис. 26 а). Якщо δ<e – труба вважається “шорсткою” (рис 26 б).

Гідравлічний коефіцієнт тертя λ є одним з найважливіших при підрахунку втрат енергії при турбулентному русі. Тому вивчений фізичних факторів, які впливають на його значення, а також ви­значення методів обчислення λ були предметом широких теоре­тичних і експериментальних досліджень. Але й дотепер ця проблема з огляду на велику складність не має розв'язаним.

У 1933 р. І. Нікурадзе опубліковані результати дослідів в трубах з різною шорсткістю.

Результати дослідів показані на рис. 27 у вигляді графіка, розглядаючи який, можна виділити чотири зони зі специфічною зміною коефіцієнта λ залежно від Re у кожній зі зон.

Зона в'язкого опору (на графіку пряма І). Ця зона відповідає ламінарному режиму. Всі експериментальні точки незалежно від відносної шорсткості лягають в логарифмічній системі координат на одну пряму, рівняння якої λ = 64/Re. Таким чином, експериментально підтверджується зроблений раніше теоретичний висновок про те, що при ламінарному режимі коефіцієнт λ не залежить від шорсткості і змінюється тільки зі зміною Re, тобто λ = f (Re). Нагадаємо, що втрати енергії в цій зоні пропорційні швидкості у першому степені.

Рис. 27. Графік Нікурадзе.

Зона гладкостінного опору (на графіку пряма ІІ ). Потік у цій зоні перебуває в умовах турбулентного руху, коефіцієнт λ не за­лежить від шорсткості та змінюється зі зміною Re, тобто λ = f (Re).

Характеристиками шорстких труб, як вже відмічалось, є абсолютна геометрична шорсткість Δ або e - висота виступів (мм) і відносна шорсткість e.

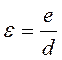. (2-57)

Для характеристики шорсткості використовують також величину

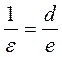. (2-58)

Коефіцієнт λ достатньо добре описується емпіричною формулою Блазіуса

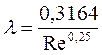, (2-59)

а також формулою

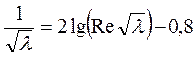. (2-60)

Усі виступи шорсткості в даному випадку вкриті в'язким прошарком, тобто δ_л>Δ. Втрати енергії в зоні гладкостінного опору пропорційні швидкості в степені 1.75.

Зона доквадратичного опору (на графіку вона показана між пря­мою і штриховою лінією аb). Коефіцієнт λ тут залежить від Δ/r₀ і Rе, тобто λ = (Rе, Δ/r₀). Усі криві (за виключенням верх­ньої) мають деякі западини, де λ зі збільшенням Rе дещо змен­шується, а далі знову зростає і наближається до постійної вели­чини.

У цій зоні певна частина виступів шорсткості вклинюється в турбулентну течію, викликаючи додаткові вихроутворення. Показ­ник степеня у формулі для визначення втрат енергії змінюється в межах 1,75 ... 2,0.

Зона квадратичного опору (вправо від штрихової лінії ab). У цій зоні всі дослідні криві ідуть майже паралельно до осі абс­цис, тобто λ = f (Δ/r₀). Отже, коефіцієнт λ стає залежним тільки від відносної шорсткості і не залежить від числа Рейнольдса, що означає автомодельність. Коефіцієнт опору для цієї зони достат­ньо добре описується формулою

. (2-61)

Втрати енергії в цій зоні пропорційні квадрату швидкості. Наведені нижче формули Прандтля Нікурадзе (2-60) і (2-61) одержуються як часткові випадки формули Альтшуля, яка має вигляд

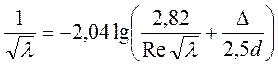. (2-62)

Знехтувавши другим членом в дужках, приходимо до формули (2.60), а при дуже великих числах Rе, знехтувавши першим чле­ном, – до формули (4.61).

На рис. 28 зображений графік для визначення коефіцієнта λ в трубопроводах з природною шорсткістю. Цей графік відрізня­ється дещо від графіка Нікурадзе (рис.27), що пояснюється впливом на потік природної шорсткості.

Для інженерних розрахунків останнім часом запропоновано ряд напівемпіричних та емпіричних формул для розрахунку коефі­цієнта λ в різних зонах опорів. Так, поряд з формулою (2.60), застосування якої рекомендується до чисел Rе < 10⁵, а також (2.62), можна

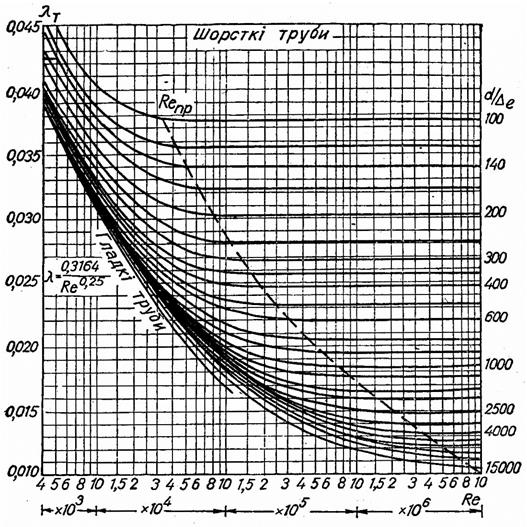
Рис. 28. До визначення коефіцієнту тертя.

скористатися для зони гладкостінного опору про­стою і зручною в розрахунках формулою, запропонованою П. К. Конаковим:

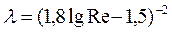. (2-63)

Ця формула має теоретично обґрунтовану структуру і є ре­зультатом обробки дослідних даних Нікурадзе. Формула Конакова, як і формула (4.60), дає задовільні результати в усьому діапазоні зміни Re.