Общее определение абстрактного векторного пространства.

V ≠ 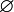; a, b, c є V; P-числовое поле.

Пусть: 1.Задана операция ∆, которая каждому a є V и каждому λ є P ставит в соответствие элемент λ∆a є V.

2. ∀ a,b є V задана операция □, которая каждой упорядоченной паре a,b є V ставит в соответствие единственный элемент a□b є V.

При этом выполняются 8 свойств (аксиом).

1. a□(b□c)=(a□b)□c

2. Ǝ z є V | ∀ a є V |a□z=z□a=a

3. ∀ a Ǝ n | n□a=a□n=z

4. a□b=b□a

5. (α+β)∆a=(α∆a)□(β∆a)

6. α∆(a□b)= (α∆a)□(α∆ b)

7. α∆(β∆a)= (αβ)∆a

8.1∆a=a

∀ a, b є V; α,β є P; 1 є P

Тогда множество V называется векторным пространством над полем Р, операция □=+, ∆=умножение вектора на число, z-единичный элемент=0, а его элементы-векторы.