Операции над матрицами

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij

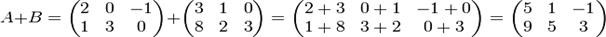
Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij - b_ij

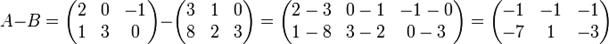
Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения 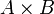) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

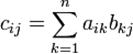
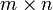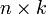В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть .

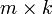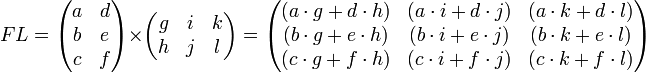
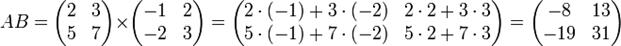
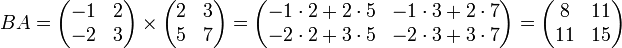
Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

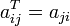
Если A — матрица размера 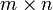, то A^T — матрица размера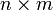

Свойства операций над матрицами

Ассоциативность сложения: A + (B + C) = (A + B) + C.

Коммутативность сложения: A + B = B + A.

Дистрибутивность умножения относительно сложения:

A(B + C) = AB + AC;

(B + C)A = BA + CA.

Свойства операции транспонирования матриц:

(A^T)^T = A

(AB)^T = B^TA^T

(A ^{− 1})^T = (A^T) ^{− 1}, если обратная матрица A ^{- 1} существует.

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

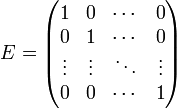
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A ^{- 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E