Понятие определителя

Матрица - это прямоугольная таблица, составленная из чисел. Особое место среди матриц занимают квадратные матрицы. Рассмотрим произвольную квадратную матрицу порядка 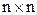или просто :

.

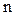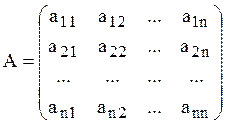Оказывается, что с такой матрицей всегда можно связать вполне определенную числовую характеристику.

Определение 1. Численная характеристика квадратной матрицы называется ее определителем.

Рассмотрим матрицу первого порядка .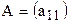

Определение 2. Численной характеристикой матрицы первого порядка, то есть определителем первого порядка, называется величина ее элемента .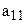

Обозначается определитель одним из символов .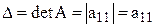

Определение 3. Определителем второго порядка, соответствующим матрице второго порядка, называется число, равное .

Обозначается определитель одним из символов

.

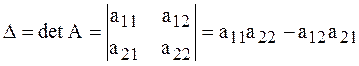Очевидно, что для составления определителя второго порядка, необходимо найти разность произведения элементов, стоящих на главной диагонали матрицы, и произведения элементов, стоящих на побочной диагонали этой матрицы.

Поскольку одна из форм обозначения определителя и обозначения матрицы имеют много общего (записывается таблица из чисел), то так же, как и у матрицы, говорят о столбцах, строках и элементах определителя.

После того как рассмотрены определители 1-го и 2-го порядков, можно перейти к понятию определителя любого порядка. Но перед этим введем понятие минора.

Определение 4. Минором любого элемента 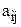квадратной матрицы порядка 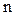называется определитель порядка 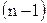, соответствующий той матрице, которая получается из первоначальной матрицы в результате вычеркивания 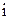-ой строки и 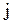-го столбца, на пересечении которых стоит элемент .

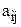Обычно минор элемента 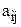обозначается .

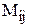Определение 5. Определителем порядка 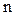, соответствующим матрице порядка 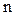, называется число, равное

.

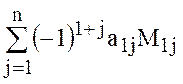Обозначается определитель одним из символов

.

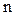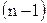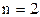Приведенное выражение представляет собой правило вычисления определителя -го порядка по элементам первой строки соответствующей ему матрицы и по минорам элементов этой строки, которые являются определителями порядка . Для это правило дает:

.

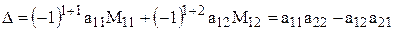В приведенном правиле вычисления определителя фигурирует лишь первая строка. Возникает вопрос, а нельзя ли вычислить определитель, используя элементы других строк?

Теорема 1. Каков бы ни был номер строки 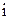( 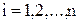), для определителя 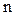-го порядка справедлива формула

,

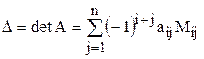называемая разложением этого определителя по 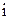-ой строке.

Нетрудно заметить, что в этой формулировке степень при (-1) равна сумме номеров строки и столбца, на пересечении которых стоит элемент .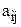

Докажем сначала эту теорему для 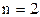. В этом случае 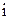может быть равно только 2, так как 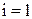входит в основное определение величины определителя. Итак:

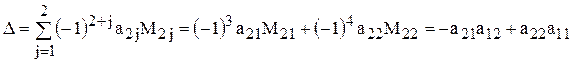
Полученное выражение совпадает с тем, которое было дано в определении, следовательно, для определителя 2-го порядка теорема доказана.

Для произвольного 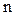данная теорема доказывается методом математической индукции.

Итак, показано, что определитель может быть разложен по любой строке. Возникает вопрос, а нельзя ли сделать то же самое, использовав произвольный столбец.

Теорема 2. Каков бы ни был номер столбца 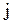( 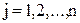), для определителя 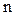-го порядка справедлива формула

,

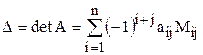называемая разложением этого определителя по 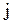-му столбцу.

Докажем теорему для :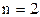

Данное выражение равно величине определителя, введенной по определению.

Итак, на основании теорем можно сказать, что для вычисления определителя 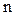-го порядка необходимо его разложить по произвольной строке или столбцу.