Постановка задачи. Нехай дано лінейнє діференціальнє рівняння (ЛДР) другого порядку

Нехай дано лінейнє діференціальнє рівняння (ЛДР) другого порядку

Y"+P(x)Y'+g(x)Y=f(x) (6.1)

де P(x),g(x),f(x)-відомі неперервні на відрізку [a,b] функції.

Лінейна крайова задача состоїть в знаходженні функції Y=Y(x), яка всередені відрізку [a,b] задоволняє рівнянню (6.1),а на його кінцях - лінейним крайовим умовам.

A0.Y(a)+A1.Y'(a)=A

B0.Y(a)+B1.Y'(a)=B (6.2)

де A0,A1,B0,B1-задані постійні,причому A0,A1,B0,B1 не дорівнюють одночасно нулю ( ).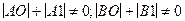

Якщо A = B = 0, то крайові умови (6.2) називаються однорідними. Лінейна крайова задача називаїться однорідною,якщо однорідні діференціальне рівняння (6.1) (f(x)=0) і крайові умови (6.2).

Оскільки умови (6.2) повинні виконуватись в двох точках - на кінцях

інтервалу [a,b],їх називають двохточечними крайовими умовами, а крайову задачу - двохточечною крайовою задачею.

Точне рішення крайової задачи можливе в рідких випадках.Тому на практиці часто використовують приблизні методи рішення, які можна розбити на дві групи: а) аналітичні; б) різністні.

Роздивимося один із різністних методів – метод кінцевих різностей.

6.2. Метод кінцевих різностей

Одним із найбільш простих методів рішення лінейної крайової задачи(6.1-6.2) являїться зведення її до системи кінцево–різностних рівнянь.

Класичне знаходження похідної функції однієї змінної записується в виді:

dY Y(x+h)-Y(x)

-- = lim -----------

dX h

Звичайно, на ЕОМ ми не можемо провести граничного переходу. З другої

сторони, ми можемо надати h деяке мале хоч і ненульове значення і перевірити,

що приближення одержується досить точним(проблема точності) і що помилка не збільшуїться в ході процесу обчислювань (проблема утриманності).

Цей метод (кінцевих різностей) зводиться до того,що ми замінюїмо похідну

різністью.

Розіб'ємо відрізок [a,b]на n рівних частин довжиною h (шаг).

b-a

h= ---

n

Позначимо точки ділення відрізка [a,b] Xo=a;Xn=b; Xi=Xo+i.h(i=1,2,...,n-1);

Pi=P(Xi);Ji=J(Xi);fi=f(Xi);Yi=Y(Xi);Yi'=Y'(Xi);Yi"=Yi"(Xi).

Замінимо приблизно в кожній внутрішній точці Xi відрізка [a,b] похідні

Yi' і Yi" кінцево – різністні відношеннями.

Y^’_i = ( Y_i+1 - Y_i ) / h ; Y’’ = (Y_i+1 - 2Y_i + Y_i-1)/ h² (6.3)

Для граничних точок Xo=a і Xn=b надамо:

Y’₀ = (Y₁ - Y₀) / h ; Y’ = (Y_n - Y_n-1 )/ h (6.4)

Використовуючи формули (6.3) і (6.4), приблизно замінимо рівняння (6.1) і крайові умови (6.2) системою n+1 лінейних алгебраїчних рівнянь з n+1 невідомими Y₀,Y₁,Y₂,...,Y_n, які являють собою значення шуканої функції Y=Y(x) в точках X₀,X₁,X₂,...,X_n:

(Y_i+2 - 2Y_i+1 + Y_i) / h² + Pi ( Y_i+1 - Y_i ) / h + gi.Yi=Fi;

( i=0,1,2,...,n-2)

A0.Y₀+A1 (Y₁ - Y₀) / h =A; B0.Y_n+B1(Y_n - Y_n-1 )/ h =B; (6.5)

Розв'язавши цю систему, можна одержати таблицю приблизних значень

шуканої функції Y=Y(x).

На практиці часто похідні Yi' і Yi" в внутрішніх точках Xi відрізка

[a,b] замінюють центрально – різностними відношеннями:

Y^’_i = (Y_i+1 - Y_i-1) /2h ; Y’’ = (Y_i+1 - 2Y_i + Y_i-1)/ h² (6.6)

а для граничних точок Xo=a і Xn=b також справжні формули (6.4). Тоді система

рівнянь для находження Y₀,Y₁,Y₂,...,Y_n, приймає вид:

(Y_i+2 - 2Y_i+1 + Y_i) / h² + Pi ( Y_i+1 - Y_i-1 ) / 2h + gi.Yi=Fi;

( i=1,2,...,n-1)

A0.Y₀+A1 (Y₁ - Y₀) / h =A; B0.Y_n+B1(Y_n - Y_n-1 )/ h =B; (6.7)

Для оцінки похибки метода кінцевих різниць на практиці часто використовують слідуючий приблизний вираз:

Yi -Y(Xi)=1/3[Yi (6.8) -Yi] (6.8)

де Y(xi)-значення точного рішення крайової задачи в точці X=Xi;

Yi -значення приблизногорішення,обчисленного в точці X=Xi з кроком h ;

Yi -значення приблизного рішення,обчисленного в точці X=Xi з кроком h/2;

Щоб знайти приблизне рішення крайової задачи з заданною точністю

E, необхідно провести обчислювання з кроком h і h/2 b зрівняти полученні

результати. Якщо [Yi -Yi]<3.E, то, з цього випливаї,[ Yi -Y(Xi)]<E і значення

Yi (i=1,2,...,n) можна прийняти за рівняння краївої задачи.