ОБРОБКА ЕКСПЕРИМЕНТАЛЬНИХ ДАНИХ

3.1. Задачі, які виникають при обробці експериментальних даних

Експериментальні дані,отримані у лабораторних або промислових умовах, являються основою для проведення подальших досліджень.В результаті проведення експерименту дослідник одержує деяку таблицю значень функції при фіксованих значеннях аргументу (табл.3.1)

Таблиця 3.1

Таблиця експериментальних значень.

При обробці експериментальних даних можуть виникнути 2 класи задач:

1.Для функції, заданої таблично, потрібно обчислити значення даної функції для проміжного значення аргументу. Цей клас задач розв'язується методом інтерполіровання.

2.Для функції, заданої таблично або графічно, підібрати аналітичну формулу, яка зображує з якоюсь точністю дані значення функції. Такі формули називаються емпирічними. Задачі даного типу вирішуються методом апроксимації.

3.2. Інтерполіровання

3.2.1. Інтерполіровання функцій

Нехай деяка функція Y=F(X) задана таблицею (табл.1), тобто при значеннях аргументу X=x₀,x₁,..,x_N функція F(X) приймає відповідно значення y₀, y₁,.., y_N. Та нехай необхідно визначити значення Y=F ( 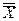) (x_i-1< 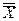< x_i). Значення x= 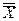попадають між двома значеннями, тому для обчислювання значення функції необхідно припустити деякий характер її зміни між відомими значеннями. Інтерполіровання можна розглядати як процес визначення для даного аргументу X значення функції Y=F(X) по її кількома відомим значенням.

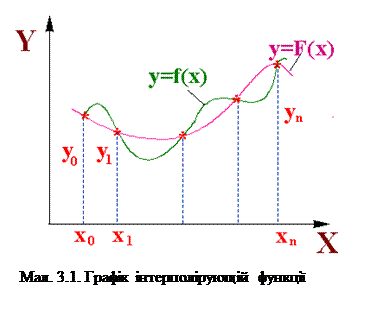Задача інтерполіровання міститься у наступному. На відрізкі [a,b] задаються n+1 точки x₀,x₁,..,x_N, які називаються вузлами інтерполяції, та значення деякої функції F(X) в цих точках

F(x₀)=y₀ ; F(x₁)=y₁ ; .... ; F(x_N)=y_N ;

Потрібно побудувати функцію Pn(X) (інтерполірующую функцію), яка б задовольнила наступним умовам:

Pn(x₀)=y₀ ; Pn(x₁)=y₁ ; ... ; Pn(x_N)= y_N;

тобто інтерполірующа функція Pn(x) повинна приймати теж саме значення, що і іскома функція F(x) для вузлових значень аргументу x₀,x₁,..,x_N .

Геометрично це означає, що потрібно знайти криву y=Pn(X) деякого визначеного типу, проходячу через дану систему точек М_i(x_i,y_i) (i=0,1,2,...,n). Очевидно,можна побуду-вати безліч безперервних функцій, які будуть проходити через дані вузлові точки (мал. 3.1).

У загальному випадку залежність, якої підпорядковується функція, може бути апроксимована многочленом n-ої степені

Pn(x) = y = a₀+a₁x+a₂x²+...+a_Nx^N= (3.1)

Тоді,для визначення коефіцієнтів многочлену (3.1) необхідно мати n+1 вузлову точку. Аналітичне визначеня коефіцієнтів інтерполяційного многочлену для n+1 точки зводиться до рішення системи лінійних рівнянь n+1 порядку, кожне з яких зображує собою вираження (3.1), записане для визначенної вузлової точки

y_i = a₀ + a₁x_i + a₂x_i² +...+ a_Nx_i ^N (i=1,2,...,n+1) (3.2)

наявності ЕОМ та відповідних програм.У бібліотеці прикладних програм ХТФ ОПУ є в наявності програми для рішення систем лінійних рівнянь методами Гаусса (SOLVE) та Зейделя (SOLVZE), якими можна користуватися при рішенні цієї задачі.

Висловлений метод не являється єдиним спосібом побудування інтерполяційного п Цим методом побудування інтерполяційного поліному зручно користуватися при оліному.Другий підхід,який часто використовують на практиці,називається методом Лагранжа.

Хай при X = x₀,x₁,..,x_N функція F(x) приймає відповідно значення y₀,y1,..,y_N. Многочлен степені не вишче n, приймаючий в вузлових точках задані значення,має вигляд:

P(x) = y = 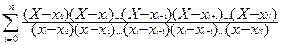*Y_i (3.3)

Цей многочлен (3.3) називається інтерполяційною формулою Лагранжа та має такі властивості:

1.При заданої сукупністі вузлових точек побудування многочлену можливо тільки єдиним спосібом.

2.Многочлен Лагранжа може бути побудован при будь-яком розміщенні вузлов інтерполяції (включаючи і нерівномірний).

У розгорнутому виді форма Лагранжа має вигляд:

(X-x₁)(X-x₂)(X-x₃)...(X-x_N) (X-x₀)(X-x₂)(X-x₃)...(X-x_N)

Рn(x)= --------------------------------- y₀ + ---------------------------------- y₁+

(x₀-x₁)(x₀-x₂)(x₀-x₃)...(x₀-x_N) (x₁-x₀)(x₁-x₂)(x₁-x₃)..(x₁- x_N)

(X-x₀)(X-x₁)...(X-x_i-1)(X-x_i+1)...(X- x_N) (X-x₀)(X-x₁)(X-x₂) ... (X-x_N-1)

+ ... + -------------------------------------------- y_i + ... + ---------------------------------------- y_N (3.4)

(x_i-x₀)(x_i-x₁)...(x_i-x_i-1)(x_i-x_i+1)...(x_i- x_N) (x_N-x₀)(x_N -x₁)(x_N -x₂) ...(x_N -x_n-1)

При n=1 формула Лагранжа набуває вигляд :

X-x₁ X-x₀

P1(X) = ------- y₀ + ------- y₁ (3.5)

x₀-x₁ x₁-x₀

та називається формулою лінійної інтерполяції.

При n=2 одержуємо формулу квадратичної інтерполяції

(X-x₁)(X-x₂) (X-x₀)(X-x₂) (X-x₀)(X-x₁)

Р2(X) = ---------------- y₀ + ----------------- y₁ + -----------------y₂ (3.6)

(x₀-x₁)(x₀-x₂) (x₁-x₀)(x₁-x₂) (x₂-x₀)(x₂-x₁)

3.2.2 Зворотне інтерполіровання

Нехай функція y=F(x) задана таблично.Задача зворотного інтерполіровання міститься у тому , щоб по заданому значенню функції Y визначити відповідне значення аргументу Х. Дана задача може бути вирішена за допомогою інтерполяційної формули Лагранжа (3). Тоді одержуємо:

X = 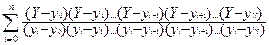*X_i (3.7)

3.3. Апроксимація

При обробці експериментальних даних інтерполяційні формули не завжди зручні. По-перше, при великом числі точек інтерполірующі поліноми мають високу степень, що з одного боку робить їх незручними, а з другого - із-за великої величини окремих доданків поліному можуть виникнути помилки округлювання. По-друге, експериментальні дані, як правило, мають помітний разброс по точністі вимірювання, особливо на кінцях відрізку визначення функції. Тому навряд чи розумно завжди будувати інтерполяційний поліном користуючись умовою збігу значень функції в усіх вузлових точках. Доцільно скористуватися деякою функціональною залежністю, параметри якої визначаються з умови мінімуму відхилення розрахункових та експериментальних значень.

Якщо вид залежності заздалегідь відомо, то задача зводиться до знайдення найкращих значень параметров цієї залежності. У протилежному випадку необхідно спочатку визначити вид цієї залежності, а потім - її параметри.

Якщо вид залежності Y=F(X) заздалегідь не відом, то користуючись визначеними міркуваннями (фізичний зміст залежності, простість емпирічної формули та т.п.) визначають вузький клас функцій, якому повинна належати іскома залежність.

Після того, як вибран клас наближающих функцій, необхідно з нього вибрати одну визначену функцію, скористаючись відповідними методами та деякими критеріями оцінки степені наближення.

3.3.1. Вибір емпирічної формули. Метод вирівнювання

В деяких випадках вибір типу емпирічної формули може бути зроблен на основі теоретичних уявлень о характері вивчаємої залежності. В інших випадках доводиться підбирати формулу, порівнюя криву, побудовану по даним спостережень, з типовими графіками формул. Такі графіки приведени в довідниках. Інколи виявляється, що емпирічна крива схожа на декілька кривих, рівняння яких різні. Зміна чисельних коефіцієнтів, які входять у формулу, часто різко змінюють вид її графіку. Вибір масштабу координатних осєй відображується на формі побудованної кривої, що також може привести до відзнаки експериментальної кривої від графіку цілком відповідной їй формулі.

Тому, раніше ніж визначати числені значення коефіцієнтів у вибраній емпирічній формулі, необхідно перевірити можливість її використання методом вирівнювання. Тільки після цього можна перейти до відшукування тих значень постійних коефіцієнтів, які дають найкращі наближення експеримен-тальних та обчислювальних величин.

Метод вирівнювання заключається у перетворюванні функції y=U(x) таким чином, щоб перетворити її у лінійну функцію. Досягається це спосібом заміни перемінних Х та Y новими перемінними X = G(x,y) та Y = Q(x,y), які вибираються так, щоб отримати рівняння прямої лінії:

Y = А + ВХ (8)

Обчислив значення X_i та Y_i за даними X_i та Y_i, наносять їх на графік з прямокутними координатами (X_i, Y_i). Якщо побудовані таким чином точки розташeвуються близько прямої лінії, то вибрана емпирічна формула y=U(x) підходить для характеристики залежності Y=F(X).

Приклад: При вивченні швидкісті химическої реакції одержани наступні дані залежності

y = f ( 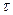) (табл. 3.1)

Таблиця 3.1.

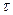
y	57.6	41.9	31.0	22.7	16.6	12.2	8.9	6.5
Y.102	1.74	2.39	3.23	4.41	6.02	8.2	11.2	15.4
X.103	33.3	16.7	11.1	8.3	6.7	5.6	4.8	4.2
Y=lgy	1.76	1.62	1.49	1.36	1.22	1.09	0.95	0.81
Y=lny	4.054	3.735	3.434	3.122	2.809	2.501	2.186	1.872

де 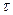- час,

y – кількість речовини в реакційний суміши к моменту .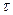

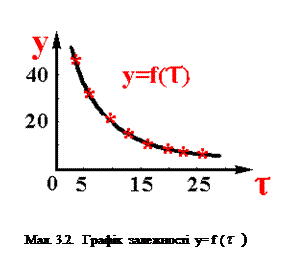Тіж самі дані зображені на малюнку 3.2.

Перевірим можливість використання 2-х формул для описання цій залежністі

а) y = 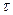/ (a+b ) ;

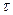b) y = a epx (b ).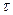

a) 1) Використовуя метод вирівнювання,

перетворим її у лінійну функцію:

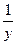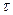= a / +b;

Введемо нови перемінни Y та X:

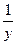Y= ; X=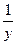

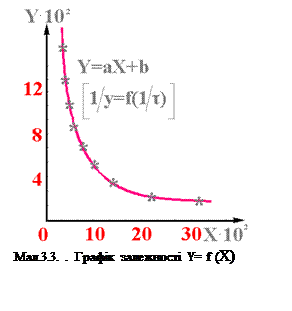
Тоді: Y = aX+b.

2) Розраховуваєм нові перемінні X та Y та занесемо їх до табл. 3.1.

3) Будуєм графік Y = aX+b.

4) Полученні крапки не уміщаються на пряму, одже цім виразом не можно описати експериментальні дані (мал. 3.3.).

б)Перевірим другу формулу y = a epx (b ).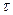

1) Використовуя метод вирівнювання, перетворим її у лінійну функцію:

ln y =ln a + b 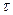або lg y= lg a + .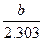

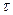Введемо нову перемінну Y :

Y = lg y

2. Обчислюєм нову перемінну Y = lg y та занесем її до табл. 3.1.

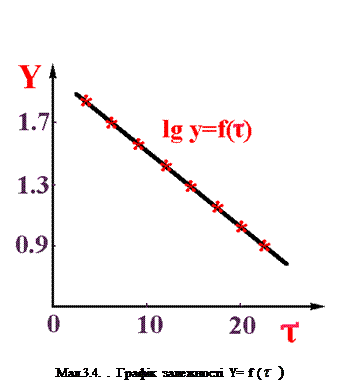
3. Будуєм графік lg Y = f ( 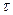) (мал. 3.4).

Видно , що крапки добре уміщаються на пряму, що доказує вживання формули б).

3.3.2.Визначення параметрів емпирічноі формули

Після того як вигляд емпирічноі залежності обран, вирішується задача визначення найкращіх коефіцієнтів(параметрів), які знаходяться у цій формулі. Як правило, пошук параметрів здійснюється для емпирічноі формули, котра приведена до лінійного виду. В основному приміняють три методи: метод обраних точок, метод середніх та метод найменьших квадратів. Останній метод найбільш точний, але і найбільш громіздкий. Тому його використовують при обробці дослідних даних високоі точності, коли необхідно отримати дуже точні значення параметрів.