Метод Ейлера-Коши
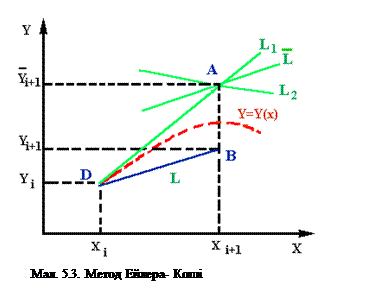
В цьому методі також використовується оцінка поведінки інтегральной кривой в послідуючих точках. Сутність метода Ейлера-Коши міститься в наступному (мал. 5.3).
За допомогою метода Ейлера (5.6) відшукуеться точка А(Xi+h,Yi+h*Yi') - для чого в точці Д(Xi,Yi) проводимо дотичну L1 до перетинання з ординатою, яка всановлена в точці Xi+1=Xi+h.
В точці А знову обчислюеться тангенс кута нахилу дотичної і проводимо її. В точці А проводимо пряму  , тангенс кута нахилу якої є середнє арифметичнем тангенсів кутів нахилу дотичних L1 i L2.
, тангенс кута нахилу якої є середнє арифметичнем тангенсів кутів нахилу дотичних L1 i L2.
Через точку Д(Xi,Yi) проводимо пряму L, паралельну  .Точка, в котрій пряма перетне ординату, востановлену в точці Xi+1=Xi+h, і буде шуканою точкою в(Xi+1,Yi+1) . Формула метода Ейлера-Коши маї слідуючий вигляд:
.Точка, в котрій пряма перетне ординату, востановлену в точці Xi+1=Xi+h, і буде шуканою точкою в(Xi+1,Yi+1) . Формула метода Ейлера-Коши маї слідуючий вигляд:
Yi+1=Yi+h/2*[f(Xi,Yi)+f(Xi+h,Yi+h*Yi')] (5.10)
Інтегрування по методу Ейлера-Коши міститься в послідовному застосуванні формул (5.6) i (5.10), починаючи з І=1. Спочатку, по (5.6) обчислюють приблизнї значення YPi+1. Потім, визначивши YPi+1, по (5.10) обчислюють шукане Yi+1. Даний метод,т акож як і модифікований метод Ейлера, має другий порядок точності.
ПРИКЛАД.
Користуючись методом Ейлера-Коши, розв'язвти рівняння (5.8) з пер вісною умовою Y(0)=0, на відрізку [0; 4], крок h=1.
РІШЕННЯ: Результати обчислень приведенні в табл. 5.3.
Таблиця 5.3
Рішення рівняння (5.8) методом Ейлера-Коши
| i | Xi | Yi | Yi’= =f(Xi,Yi) | Xi +1 = =Xi+h | YPi+1= Yi+h*Yi’ | YP’i+1= f(Xi +1, YPi+1) | h*( Y’i+ +YP’i+1)/2 |
| 0.05 | 0.05 | 0.0473 | 0.0486 | ||||
| 0.0486 | 0.0473 | 0.0959 | 0.0446 | 0.0460 | |||
| 0.0945 | 0.0446 | 0.139 | 0.0421 | 0.0434 | |||
| 0.138 | 0.0421 | 0.180 | 0.0398 | 0.0410 | |||
| 0.179 |
5.1.5. Методи Рунге-Кутта
Найбільш поширеними у практиці інтегрування звичайних диференційних рівнянь є методи Рунге-Кутта різноманітного порядку точності. Перевагою ціх методів є те, що при їх використовуванні не треба обчислювати похідні вищє першого порядку, а їх головний недолік - значний об'єм обчислень на кожному році.
До методів Рунге-Кутта відносяться метод Ейлера - метод Рунге-Кутта пер- шого порядку точності; модифікований метод Ейлера і метод Ейлера-Коши - метод Рунге-Кутта другого порядку.
Метод Рунге-Кутта четвертого порядку точності - один із найуживаніших методів інтегрування диференційних рівнянь. Взагалі його називають просто "методом Рунге-Кутта". Цей метод описуеться системою п'яти рівнянь:
Yi+1=Yi+h/6*(K1+2*K2+2*K3+K4) (5.11)
де K1=f(Xi,Yi) (5.12)
K2=f(Xi+h/2,Yi+h*K1/2) (5.13)
K3=f(Xi+h/2,Yi+h*K2/2) (5.14)
K4=f(Xi+h,Yi+h*K3) (5.15)
Інтегрування по методу Рунге-Кутта міститься в наступному. Для кожної і-ої точки (i=1,2,..,n-1) no (5.12) - (5.15) обчислюються значення Кj (j=1,2,3,4). Потім по (5.11) послідовно визначаються значення Yi (i=1,2,..,n).
5.2. Багатоступінчати методи
5.2.1.Методи прогноза та корекції
Відмінною рисою методів Рунге-Кутта є те, що при обчислюванні слідуючої точки (Xi+1,Yi+1) використовуїться інформація тільки про точки (Xi,Yi). У методах другого порядка і вище доводиться вичисляти значення функції в одній чи кількох проміжних точках. Це не завжди раціонально, оскільки, якщо процес інтегрування вже просунувся на декілька кроків, то маїмо ту додаткову інформацію (про попередні точки рішення), для використання якої не потрібно обчислювати значення функцій.
Методи прогноза та корекції відрізняються тією властивістю, що за їх до- помогою неможливо почати рішення диференційного рівняння, тому що в них необхідно використовувати інформацію про попередні точки рішення. Для початку рішення рівняння, маючи тільки одну точку, визначену первісною умовою, необхіднє використовувати метод типу Рунге-Кутта.
З назви метода зрозуміло, що спочатку "завбачаїться" значення Y(0)i +1, а потім використовуїться той чи інший метод для "коректування" отриманного зна чення.Звичайно, після цього можна використовувати ту ж саму формулу для повторного коректування значення Yi+1. Цей ітераційний процес можна повторювати скільки завгодно разів, але з точки зору єфективності доцільно зменьшувати число ітерацій, вибираючи відповідний крок інтегрування.
Для прогноза значення Yi+1 можна використовувати різні формули. Формула другого порядку точності маї вигляд:
Y(0)i +1 =Yi-1+2*h*f(Xi,Yi) (5.16)
де верхній індекс (0) означаї первісне наближення до Yi+1, тобто завбачене значення.
З (5.16) видно, що за її допомогою неможливо обчислити Yi. Тому для обчислення Yi використовуеться метод Рунге-Кутта. Всі послідуючі точки будуть обчислятися з використанням інформації про попередні точки рішення без додаткових обчислень значення функції. Це дозволяї класифікувати методи прогноза та корекції як багатоступінчасти методи рішення диференційних рівнянь.
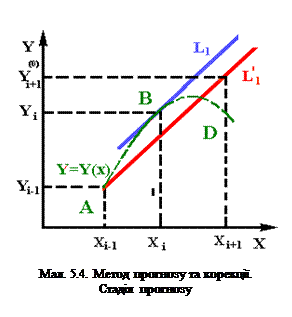
Алгоритм рішення рівняння методом прогноза та корекції слідуючий. По (5.16) обчислюється завбачене значення Y(0)i+1. Геометрично завбачення зводиться до того, що знаходимо кут нахилу дотичної в точці (Xi,Yi) (пряма L1 на мал. 5.4). Після цього через точку (Xi-1,Yi-1) проводиться пряма L’1, паралельна L1. Завбачене значення Yi+1 буде розташоване там, де пряма L’1 перетине з ординатою X=Xi+1.
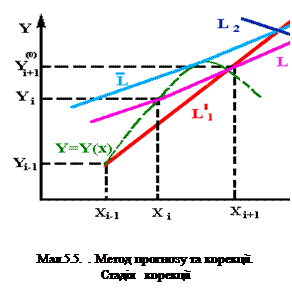 Тепер потребується деякий метод корекції завбаченого значення. Виходячи того, що величина Y(0)i+1 відома, можна обчислити нахил дотичної в точці (Xi+1, Yi+1). Ця дотична відображена на мал. 5.5 і позначена L’1. Пряма L’1 на мал. 5.5 становить собою те ж саме, що й на мал. 5.4, і усреднив тангенси кутів нахилу ліній L'1 і L2, отримуїмо лінію
Тепер потребується деякий метод корекції завбаченого значення. Виходячи того, що величина Y(0)i+1 відома, можна обчислити нахил дотичної в точці (Xi+1, Yi+1). Ця дотична відображена на мал. 5.5 і позначена L’1. Пряма L’1 на мал. 5.5 становить собою те ж саме, що й на мал. 5.4, і усреднив тангенси кутів нахилу ліній L'1 і L2, отримуїмо лінію  .Через точку (Xi,Yi) проводимо пряму L, паралельну
.Через точку (Xi,Yi) проводимо пряму L, паралельну  . Точка перетинання цієї лінії з ординатою X=Xi+1 дає нове наближення до Yi+1.
. Точка перетинання цієї лінії з ординатою X=Xi+1 дає нове наближення до Yi+1.
Назвемо це наближення зкоректованим значенням Y(1)i +1. Обчислити це зкоректоване значення можливо по формулі:
Y(1)i+1=Yi+h/2*[f(Xi,Yi)+f(Xi+1,Y(0)i+1)] (5.17)
Можна знайти нове, можливо, ще найкраще наближення до Yi+1, використо-вуючи знайдене значення Yi+1 і коректуючи знов. В загальному випадку, К-те наближення до Yi+1 обчислюється по формулі:
Y(k)i+1=Yi+h/2*[(f(Xi,Yi)+f(Xi+1,Y(k-1)i+1)] (5.18)
для К=1,2,3,... .
Ітераційний процес завершується, коли
|Y(k+1)i+1 - Y(k)i+1| < Є (5.19)
Обираючи крок для метода прогноза та корекції необхідно користуватися слідуючим емпірічним правилом : мінімальний об'їм обчислень(і, отже, мінімальні затрати машинного часу) досягаються при числі ітерацій рівним 2. Іншими словами, крок інтегрування потрібно вибирати так, щоб умова (19) виконувалась після двох ітерацій. При більшому числі ітерацій крок h необхід-но зменьшувати, в іншому випадку він може бути збільшений.
ПРИКЛАД.
Використовуючи метод прогноза та корекції, знайти з точністю Е=0.001 значення Y2=Y(2) та Y3=Y(3) рішення Y=Y(X) диференційного рівняння (8) з первісною умовою Y(0)=0. Візьмемо крок h=1.
РІШЕННЯ:Приймаючи за увагу те, що для використання формули (16)необхідна інформація про дві точки, то значення Y1=Y(1) візьмемо з попереднього прикладу, обчисленного за lопомогою метода Ейлера-Коши, Y1=0.0486. Тепер по формулі (16) обчислимо завбачене значення в точці Y(0)2 .
Y(0)2 =Y0+2*h*f(X1,Y1)=0+2*1*0.0473=0.0972
Корекцію оптимального значення виконаїмо по формулі (18). Перше наближення:
Y(1)2 =Y1+h/2*[f(X1,Y1)+f(X2,Y(0)2)]=0.0486 + 1/2*(0.0473+0.0446)=0.0944
Друге наближення:
Y(2)2 =Y1+h/2*[f(X1,Y1)+f(X2,Y(1)2)]=0.0486+1/2*(0.0473+0.0446)=0.0946
Перевірка виконання умови (19)
|Y(2)2 - Y(1)2 | < Є
В зв'язку з тим, що умова (19) виконуїться, то приймаїмо Y2=0.0946. Далі по (16) обчислюємо завбачене значення в точці Y3.
Y(0)3 = Y1 + 2*h*f(X2,Y2)=0.0486 +2*1*0.0446=0.1378
Корекцію отриманного значення виконаїмо по формулі (18). Перше наближення:
Y(1)3 = Y2 + h/2*[f(X2,Y2) + f(X3,Y(0)3)]= 0.0946 + 1/2*(0.0446 +0.0421)=0.1380
Друге наближення:
Y(2)3 = Y2 + h/2*[f(X2,Y2)+f(X3,Y(1)3)]= 0.0946 +1/2*(0.0446 + 0.0421)=0.1380
Перевірка виконання умови (9.19)
|Y(2)3 - Y(1)3 | < Є
В зв'язку з тим, що умова (19) виконуїться, то приймаїмо Y=0.1380
Метод прогноза та корекції ї більш точним,ніж раніш розглянені методи
другого порядку точності.
6. МЕТОДИ РІШЕННЯ ЛІНЕЙНОЇ КРАЙОВОЇ ЗАДАЧИ
ДЛЯ ЗВИЧАЙНИХ ДІФЕРЕНЦІАЛЬНИХ РІВНЯНЬ
Дата добавления: 2015-08-26; просмотров: 903;
