Метод обраних точок
Нехай емпирічна формула має вид (8).Потрібно знайти значення коефіцієнтів А та В.
Наносимо на координатну площину дослідні точки (xi, yi), що найближче до цих точок проводимо пряму (приблизна пряма). На цій прямій обираємо дві (за кількістю параметрів) довільні точки N1(x1",y1") та N2(x2",y2"), не обов'язково співпадаючі з точками (xi,yi) і як найдалі віддалені одна від одноі. Координати цих точок підставляємо в рівняння (8), після чого отримуємо систему:
y1"=A.x1"+B
y2"=A.x2"+B
Розв'язуючі систему,знаходимо A і B.
3.3.2.2. Метод середніх
Нехай емпирічна формула має вид (8). Підставляємо у цю формулу замість X і Y дослідні значення x і y. Так як ліва частина формули як правило не рівняється правій, отримуємо систему рівнянь:
A.x1+B - y1= Є1;
A.x2+B - y2= Є2; (9)
.........................
A.xn+B - yn= Єn;
де Є1, Є2,..., Єn - непогодження (відхилення), які можуть бути як позитивними, так і негативними.
Згідно методу середніх, за найкращу емпирічну залежність приймається та,
яка забезпечує нульове значеня суми відхилень по всім експериментальним точкам, тобто алгебраічна сума непогоджень дорівнює нулю
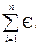 = 0 (10)
= 0 (10)
Визначення параметрів A і B формули (8) роблять таким чином:
1.Складають умовні рівняння yi=A.xi+B,число яких m дорівнює числу власних значень xі і yі.
2.Умовні рівняння розділяють на приблизно рівні групи, число яких n дорівнює
числу визначаємих коефіцієнтів (в даному випадку -2).
3.Рівняння, які входять до кожноі з цих груп, додаються. Для даного випадку одержуємо два рівняння:
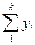 = A.
= A. 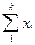 + k.B;
+ k.B;
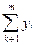 = A.
= A. 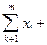 (m - k).B (11)
(m - k).B (11)
4.З цих рівнянь знаходять невідомі коефіцієнти A і B.
Групування умовних рівнянь перед іх підсумовуванням можа провести різними способами, причому кожний з них дає декілька відрізняючих значень коефіцієнтів. Рекомендується згуртовувати рівняння за порядком монотонноі зміни однієі з підставних.
3.3.2.3. Метод найменьших квадратів
Емпирічна формула в загальному вигляді може бути записана так:
Yі=F(xi, Aj)
де xi - незалежні підставні;
Aj - коефіцієнт емпирічноі залежності.
Згідно з методом найменьших квадратів найкращими коефіцієнтами у смислі приближення до експериментальних даних (yi=f(xi)), будуть коефіцієнти, відшукані з умови
min[R(Aj)] = 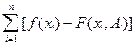 2 (i = 1, 2, ..., n; j = 0, 1,..., m) (12)
2 (i = 1, 2, ..., n; j = 0, 1,..., m) (12)
тобто мінімума суми квадратів відхилень між експериментальними та розрахунковими значеннями.
При фіксованих значеннях x функція R(Aj) є позитивно визначеною (заданою та безперервою у інервалі [x1,xn]) функціею і, звичайно, має екстремум. Необхідною умовою для існування екстремума функціі декількох підставних є рівність нулю часних похідних по кожній підставній.
Нехай емпирічна формула має вигляд:
F(xi,A j) = a0+a1.xi+a2.xi2+...+am.xim
Тоді вираз (12) можна записати так:
R(Aj) = 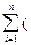 a0+a1.xi+a2.xi2+...+am.xim - yi)2 (13)
a0+a1.xi+a2.xi2+...+am.xim - yi)2 (13)
Знайдемо часні похідні функціі R(a0, a1,...,am) по a0, a1,...,am та прирівнюємо їх до нуля. Отримаємо так звану нормальну систему m+1 рівнянь з m+1 невідомими a0, a1,...,am:
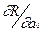 = 2
= 2 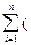 a0+a1.xi+a2.xi2+...+am.xim - yi). 1 = 0;
a0+a1.xi+a2.xi2+...+am.xim - yi). 1 = 0;
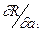 = 2
= 2 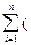 a0+a1.xi+a2.xi2+...+am.xim - yi). xi = 0; (14)
a0+a1.xi+a2.xi2+...+am.xim - yi). xi = 0; (14)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
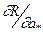 =2
=2 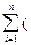 a0+a1.xi+a2.xi2+...+am.xim - yi). xi m= 0;
a0+a1.xi+a2.xi2+...+am.xim - yi). xi m= 0;
Вирішивши систему відомими методами (формули Крамера, метод Гауса та інші), знайдемо коефіцієнти a0, a1,..., am формули (12), яка буде мати найменьше квадратичне відхилення R(Aj).
На практиці, як правило, при визначенні коефіцієтів з використанням метода
найменьших квадратів будь-яку емпирічну залежність доцільно привести до лінійного виду. Розгянемо отримання системи нормальних рівнянь для цього випадку.
Потрібно визначити коефіцієнти емпирічноі формули
F(xi,Aj) = a0+a1.xi (15)
Тоді вираз (13) буде мати вигляд:\
R(xi,Aj) = 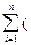 a0 + a1.xi - yi)2 (16)
a0 + a1.xi - yi)2 (16)
Нормальна система для визначення a0 та a1 буде мати такий вигляд:
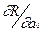 = 2
= 2 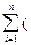 a0+a1.xi- yi). 1 = 0;
a0+a1.xi- yi). 1 = 0;
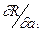 = 2
= 2 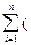 a0+a1.xi - yi). xi = 0;
a0+a1.xi - yi). xi = 0;
Зробивши прості перетворення, маємо:
a0.n + a1 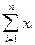 =
= 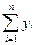
a0 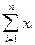 + a1
+ a1 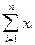 2 =
2 = 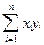 (17)
(17)
Вирішив систему (17), отримаємо значення a0 та a1. Підставив іх у формулу (15), отримаємо конкретний вид емпирічноі формули.
4. МЕТОДИ ЧИСЕЛЬОГО ІНТЕГРУВАННЯ
Чисельне інтегрування - це обчислення визначеного інтеграла по ряду чисельних значень підінтегральної функції.
Потрібно обчислити визначений інтеграл
І = 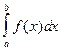 (4.1)
(4.1)
за умовою, що a і b - кінцеві та f(x) виявляється безперервною функцією Х на усьому інтервалі a<=X<=b.
Загальний підхід до рішення задачі такий. Визначений інтеграл I являє собою площу, обмеженную кривою f(x), вісью Х та ординатами у точках X=a і X=b.
Ми будемо обчислювати I, розбиваючи інтервал від a до b на безліч менших інтервалів, находити приблизно площу кожної "смуги", яка виходить при такому роздрібленні та підсумовувати площі цих смуг.
Чим менше інтервал роздріблення тим точніше буде обчислена інтервальна сума. Проте при цьому значно побільшиться кількість обчислень. Тому на практиці доводиться обмежуватись кінцевим роздрібленням інтервала інтегрування функції, допускаючи при цьому деяку помилку.
Різноманітність методів чисельного інтегрування обумовлено стратегією вибора точок роздріблення, забезпечуваючого у кожному конкретному випадку мінімально можливу помилку. Можливі два способа вибору точок роздріблення вихідного інтервала. Перший спосіб - число інтервалів фіксують заздалегіть, другий - число та розміри інтервалів визначаються у процесі обчислення інтервала виходячи з вимог заданої точності. В обох випадках вихідна функція на кожному інтервалі апроксимується відповідно залежності, наприклад, лінійноі або квадратичноі.
4.1. Метод трапецій
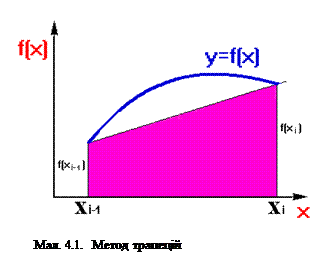 Метод трапецій заснований на тому, що графік підінтегральнї функції на кожному відрізку роздріблення замінюється стягуючьою його хордою, та площа, обмежена інтервалом роздріблення замінюється площею трапеції (Мал. 4.1). Тоді для інтегралу (4.1) на інтервалі [Xi-1;Xi] можливо записати:
Метод трапецій заснований на тому, що графік підінтегральнї функції на кожному відрізку роздріблення замінюється стягуючьою його хордою, та площа, обмежена інтервалом роздріблення замінюється площею трапеції (Мал. 4.1). Тоді для інтегралу (4.1) на інтервалі [Xi-1;Xi] можливо записати:
де правая частина виявляється площею трапеції.
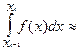
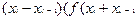
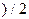 (4.2)
(4.2)
Якщо (Xi-Xi-1) = (b-a)/n =h, тоді для визначеного інтеграла виходить таке приблизне значення:
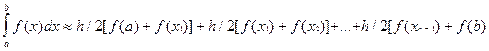 ]=
]=
= 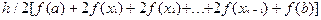 (4.3)
(4.3)
або
 (4.4)
(4.4)
де h = (b-a)/n.
 Формула (4.4) називається формулой трапеції для чисельного інтегрування. Для користування нею необхідно знати значення підінтеграль-ної функції у точках Хо; Х1; Х2 ... Хn. Якщо підінтеграль-на функція задана графічно, тоді ці значення считуються з креслення, а якщо вона задається аналітично, тоді f(Xo), f(X1),..., f(Xn) знаходяться шляхом підстави у підінтегральну функцію абсцис Хо,Х1,..., Хn.
Формула (4.4) називається формулой трапеції для чисельного інтегрування. Для користування нею необхідно знати значення підінтеграль-ної функції у точках Хо; Х1; Х2 ... Хn. Якщо підінтеграль-на функція задана графічно, тоді ці значення считуються з креслення, а якщо вона задається аналітично, тоді f(Xo), f(X1),..., f(Xn) знаходяться шляхом підстави у підінтегральну функцію абсцис Хо,Х1,..., Хn.
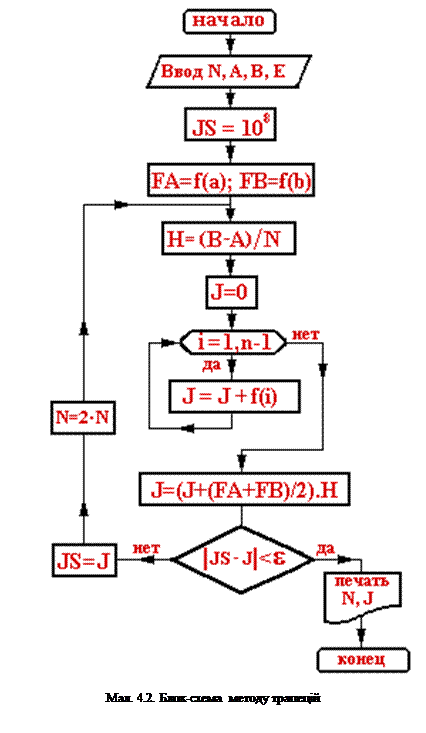
Блок-схема методу приведена на мал. 4.2.
4.2. Метод Сімпсона
Метод Сімпсона являє собою один з наібільш поширених та частіше вживаємих методів чисельного інтегрування. На відмінну від попереднього метода підінтегральна функція апроксимується у межі двох прилеглих інтервалів роздріблення квадратичною залежністью, оскільки для обчислення коефіціентів параболи необхідно мати три значення функції. Число інтервалів роздріблення при цьому потрібно бути парним.
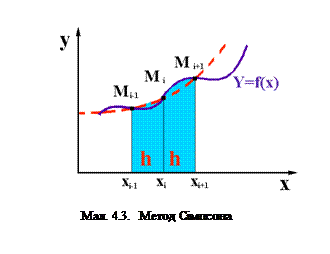 Разоб'ємо інтервал [a,b] на парне число n=2k проміжков рівної довжини h точками Хо=а; Х1; Х2;;...Х2n-1; X2n=b. Розгляним два прилеглих інтервала роздріблення [Xi-1; Xi] та [Xi; Xi+1], кожний з котрих має довжину h=(b-a)/n. Проведемо у точках Хi-1; Xi; Xi+1 ординати до перетинання з кривой Y=f(X) у точках Mi-1; Mi; Mi+1. Через ці точки проводиться парабола з осью, паралельній осі ординат OY (Мал.4.3). Для площі, обмеженой параболою на інтервалі [Xi-1;Xi+1] можливо записати:
Разоб'ємо інтервал [a,b] на парне число n=2k проміжков рівної довжини h точками Хо=а; Х1; Х2;;...Х2n-1; X2n=b. Розгляним два прилеглих інтервала роздріблення [Xi-1; Xi] та [Xi; Xi+1], кожний з котрих має довжину h=(b-a)/n. Проведемо у точках Хi-1; Xi; Xi+1 ординати до перетинання з кривой Y=f(X) у точках Mi-1; Mi; Mi+1. Через ці точки проводиться парабола з осью, паралельній осі ординат OY (Мал.4.3). Для площі, обмеженой параболою на інтервалі [Xi-1;Xi+1] можливо записати:

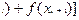
Аналогично, для слідуючого інтервала[Xi+1;Xi+3], одержим:
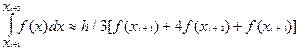
Якщо подібну операцію провести для кожної трійки точек, починая з [Xo;X2] та закінчуя
[Xn-2;Xn], тобто замінив графік вихідної функції n параболами, а потім складаючи почленно одержані формули, тоді кінцево одержим формулу Сімпсона:
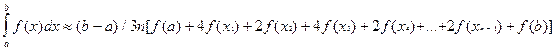 (4.5)
(4.5)
 Помітимо, що у одер-жаної суми елементи з коефіціентом 4 відповідають непарним точкам точкам, а елєменти з коефіціентом 2 - парним точкам.
Помітимо, що у одер-жаної суми елементи з коефіціентом 4 відповідають непарним точкам точкам, а елєменти з коефіціентом 2 - парним точкам.
Блок-схема методу приведена на мал. 4.4.
4.3. Оцінка точності формул чисельного інтегрування.
Вибір кроку інтегрування
Будь-яка формула інтегрування дозволяє обчислити лише приблизне значення інтервала. Тому можливо записати:
 (4.6)
(4.6)
де R- хиба використованої формули інтегрування.
Явно, помилка формули залежить від розміру крока інтегруваня, а також від класа підінтегральної функції. Чим менше крок інтегрування, тим менше помилка R. Розмір кроку інтегрування залежить від заданої точності обчислень та обраної формули інтегрування.
4.3.1. Вибір кроку інтегрування за оцінкою остаточного члена (помилки)
Відповідно обчислити оцінку помилки можливо слідуючим спосібом. Необхідно
одержати точне значення інтервала та порівняти з приблизним, обчисленим за відповідною формулою. Хибу формули доцільно оцінювати, використовуя слідуючу, більш високу ступінь підінтегральної функції, чим та, для которої вона надає точне значення інтеграла. Для формул прямокутників та трапецій це буде функція вида Y=X2 ; для формул Сімпсона- Y=X4 и т.п.
Після того, як оцінка значення помилки (R), крок інтегрування вибирається так, щоб виконувалась слідуюча нерівність:
|Rmax| < 0,5Є (4.7)
де |Rmax| максимальне значення остаточного члена.
Відповідно, розмір крока h повинен вибиратися так, щоб при максимальному значенні похідної виконувалась приведена умова (4.7):
Для формул трапецій:
0,5 Є > |Rmax| = (max |Y"(X)| / 12)*|b-a|*h2 (4.8)
Для формули Сімпсона:
0,5 Є > |Rmax| = (max |Y""(X)| / 180)*|b-a|*h4 (4.9)
4.3.2. Вибір кроку інтегрування за допомогою подвійного перерахунку
Тому що визначеня кроку інтегрування за розміром остаточного члена зводить к громіздким обчисленням, можливо використати слідуючий прийом.
За вибраною формулою (методом) інтеграл обчислюється два рази: спочатку з якимось кроком h, а потім з кроком h/2, тобто подвоюють число n. Позначим наслідок обчислень як Sn і S2n та порівняєм їх.
Якщо |Sn-S2n| < Є, де Є - допустима хиба, то вважають, що Sn=S2n. Якщо |Sn-S2n| > Є, тоді розрахунок повторюють з кроком h/4 та порівнюють |S2n-S4n| і т.п.
У ролі початкового кроку можливо рекомендувати
 h=
h= 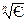
де: n=2 - для формули трапецій
n=4 - для формули Сімпсона.
ПРИКЛАД.
За допомогою формули Сімпсона обчислити 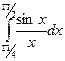 з точністю е = 10 –2 .
з точністю е = 10 –2 .
Визначим: h = 
При використанні формули Сімпсона число частин n повинно бути парним , т.є.відрізок [p/4;p/2] треба розбити на парне число рівних частин .
p/2 - p/4 = p/4 = 3.14/4 » 0.8  ; n = 0.8 ¸ 0.32 » 3. n = 3 нам не подходить, вибираємо парне значення n = 4.
; n = 0.8 ¸ 0.32 » 3. n = 3 нам не подходить, вибираємо парне значення n = 4.
Тоді : h = 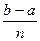 =
= 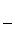 = p/16
= p/16
Перевіряємо : 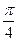 ¸
¸ 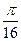 = 4 = n
= 4 = n
| in | i 2n | xi | xi (рад) | sin x i | y0,y2n | y2i+1 | y2i |
| p /4 | 0.7854 | 0.7071 | 0.9003 | ||||
| 9p/32 | 0.8836 | 0.7735 | 0.8754 | ||||
| 10p/32 | 0.9817 | 0.8323 | 0.8478 | ||||
| 11p/32 | 1.0799 | 0.8816 | 0.8164 | ||||
| 12p/32 | 1.1781 | 0.9239 | 0.7842 | ||||
| 13 p/32 | 1.2763 | 0.9572 | 0.7500 | ||||
| 14p/32 | 1.3744 | 0.9805 | |||||
| 15p/32 | 1.4726 | 0.9951 | 0.6757 | 0.7134 | |||
| 16p / 32 | 1.5708 | 1.00 | 0.6366 |
Примітка : sin x можна знайти, якщо перевести значення p у градуси або в радіани.
1.Для переведення у градуси : p = 180 0 ; p/4 = 450 ; p/16 = 110 15’
2.Для переведення у радіани : p = 3.1416 ; p/4 = 3.1416 / 4 = 0.7854…
По формулі Сімпсона при n = 4 і h = 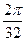 знаходимо :
знаходимо :
» 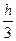 [ (y0 + y4 ) + 4 ( y1 + y3 ) + 2·y2 ] =
[ (y0 + y4 ) + 4 ( y1 + y3 ) + 2·y2 ] =  [ ( 0.9003 + 0.6366 ) + 4 (0.8478 + 0.7134 ) + 2·0.7842 ] =
[ ( 0.9003 + 0.6366 ) + 4 (0.8478 + 0.7134 ) + 2·0.7842 ] =
= 0.0654 ( 1.5369 + 6.2448 + 1.5684 ) = 0.61196.
Тепер проведемо розрахунок при n = 8 та h = 
По формулі Сімпсона при ціх значеннях отримаємо:
» 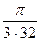 [ (0.9003 + 0.6366 ) + 4×( 0.8754 + 0.8164 + 0.6757 ) + 2(0.8478 +0.7842 + 0.7134 ) ] = 0.0982 × (1.5369 + 12.47 + 4.6908 ) = 0.61188.
[ (0.9003 + 0.6366 ) + 4×( 0.8754 + 0.8164 + 0.6757 ) + 2(0.8478 +0.7842 + 0.7134 ) ] = 0.0982 × (1.5369 + 12.47 + 4.6908 ) = 0.61188.
Визначимо
½Sn –S2n ½ = ½0.61196 – 0.61188 ½= 0.00008 < 10-2 / 2.
Таким чином, значення інтеграла дорівнює
= 0.612.

5. МЕТОДИ ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ ЗВИЧАЙНИХ
ДІФЕРЕНЦІАЛЬНИХ РІВНЯНЬ
Діференціальне рівняння установлює звязок між незалежними змінними, невідоми (шуканими) функціями та їх похідними.
Рішення діференціального рівняння n-го порядку
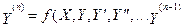 (5.1)
(5.1)
полягаї в видшуканні функції Y=Y(X), котра задовольняє (1) та початковим умовам:

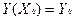 ;
; 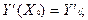
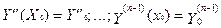 (5.2)
(5.2)
де Yo, Y'o, Y"o,...,Yo(n-1) - задані числа.
Така задача називається задачей Коши. Для звичайного діференцального рівняння першого порядку
Y' = f(X,Y) (5.3)
початкова умова маї вигляд:
Y(Xo)=Yo (5.4)
Геометричний зміст рішення цієї задачи полягає в знаходженні інтегральної кривої Y=Y(X), яка проходить через задану точку А(Xo,Yo). Рівнення (3) установлюї зв'язок між координатами та похідної від функції в наданій точці в системі координат Y-X. Отже, для будь-якої точки за (3) можливо обчислити похідну, тобто тангенс кута нахилу дотичної до кривої Y=Y(X). Інакше кажучи, рівнення (3) можливо розглядати як визначення кривої через її похідну.
Чисельне рішення задачи Коши полягаї в знаходженні значень Y1,Y2,...,Yn в точках X1=Xo+h, X2=Xo+2.h,...,Xn=Xo+n.h відрізка [a,b], де h - крок інтегрування, Xo=a, Xn=d. Нанеся точки (Xo,Yo), (X1,Y1),..., (Xn,Yn) на координатну плошину та з'єднав їх відрізками прямої, одержим ломану лінію, яка зветься ломаной Ейлера - приблизне зображення шуканої кривої (мал. 5.1)
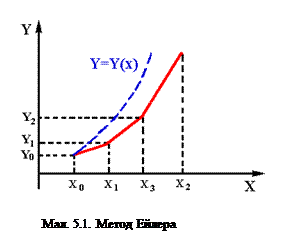 Цей метод рішення діференціального рівнення називається методом Ейлера. Цілком зрозуміло, що у цоьму найпростішому методі безліч недоліків. Ми намагаємось описати криву відрізками прямої, що може приводити до помітних хиб (як, наприклад, на мал.5.1). Очевидно, що яким-небудь спосібом необхідно облічувати кривизну шуканого рішення. Для цього розроблен ряд методів, котрі підрозділяються на два класи - одноступінчати та багатоступінчати методи.
Цей метод рішення діференціального рівнення називається методом Ейлера. Цілком зрозуміло, що у цоьму найпростішому методі безліч недоліків. Ми намагаємось описати криву відрізками прямої, що може приводити до помітних хиб (як, наприклад, на мал.5.1). Очевидно, що яким-небудь спосібом необхідно облічувати кривизну шуканого рішення. Для цього розроблен ряд методів, котрі підрозділяються на два класи - одноступінчати та багатоступінчати методи.
1.Одноступінчати методи, у котрих використовується тільки інформація про шукану криву в одній точці та не робляться ітерації. Одним з таких методів виявляється рішення рівнянь за допомогою рядів Тейлора. Практично зручними методами виявляються методи Рунге-Кутта.
2. Багатоступінчати методи, у котрих використовується інформація про криву як мінимум у двох точках та вживається ітераціонна процедура. До цих методів належать методи прогноза та корекції.
5.1. Одноступінчати методи
5.1.1. Рішення за допомогою рядів Тейлора
Методика чисельного рішення будь-якого діференціального рівнення зв'язана з розкладом рішення у ряд Тейлора у h - місцевості точки X:
Yi+1 = Yi+h.Yi' + (h2/2!)*Yi" + (h3/3!)*Yi’’’ + ... (5.5)
де Yi(k) - K-ая похідна функції Y=f(X) у точках X=Xk; h=Xi+1-Xi.
Нахoдження рішення за допомогою ряда Тейлора являється одноступінчатим методом, тому що для обчислення Yi+1 потрібна інформація тільки про одну попередню точку. Принципово (5.5) може бути використована при інтегруванні будь-якого діференціального рівняння з будь-якою наперед заданою точністью, від якої будє залежить число членів ряда. На практиці через необхідність обчисленя функції та усіх її похідних, що дуже складно, цей метод використо-вується як спосіб оцінки точності інших формул, тобто наскільки тот або інший метод погоджується з розкладом у ряд Тейлора. Деякі методи будуть погоджу-ваться до членів порядку h, другі- аж до членів порядку h4 і т.п.
Дата добавления: 2015-08-26; просмотров: 1314;
