Модификований метод Ейлера
На відміну від звичайного метода Ейлера в цьому методі використовується оцінка поведінки інтегральної кривої в наступних точках. Порядок побудови рішення в модифікованому методі Ейлера полягає в наступному.
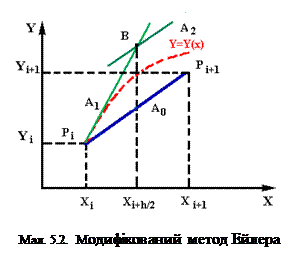 Через точку Рi(Xi,Yi) (мал. 5.2) проводиться дотична А1 з тангенсом кута нахилу f(Xi,Yi) до перетинання з ординатою в точці X=Xi + h/2 (по методу Ейлера (6)). Одержуїмо точку перетинання В з координатами (Xi+h/2, Yi+h/2*Yi'). Вираховуваем тангенс кута нахилу дотичної в цій точці: Кi=Yi'+1/2=f(Xi+h/2, Yi+h/2*Yi'). Пряма з таким нахилом, яка проходить через точку В, позначена А2. Далі, через точку Рі(Xi,Yi) проводимо пряму Ао, паралельну А2. Перетинання прямой Ао з ординатою Х=Хі+1 і дае шукану точку Рі+1(Xi+1,Yi+1).
Через точку Рi(Xi,Yi) (мал. 5.2) проводиться дотична А1 з тангенсом кута нахилу f(Xi,Yi) до перетинання з ординатою в точці X=Xi + h/2 (по методу Ейлера (6)). Одержуїмо точку перетинання В з координатами (Xi+h/2, Yi+h/2*Yi'). Вираховуваем тангенс кута нахилу дотичної в цій точці: Кi=Yi'+1/2=f(Xi+h/2, Yi+h/2*Yi'). Пряма з таким нахилом, яка проходить через точку В, позначена А2. Далі, через точку Рі(Xi,Yi) проводимо пряму Ао, паралельну А2. Перетинання прямой Ао з ординатою Х=Хі+1 і дае шукану точку Рі+1(Xi+1,Yi+1).
Рівняння прямої Ао можно записати:
Yi+1=Yi+Ki*(Xi+1-Xi)=Yi+h*f(Xi+h/2,Yi+h/2*Yi') (5.9)
Формула (5.9) описуе модифікований метод Ейлера. Інтегрування за модифікованим методом Ейлера міститься у послідовному застосуванні формул (5.6) (при h=h/2) і (5.9) до рівняння (5.3), починаючи з I=1. Цей метод є більш точним (другого по рядку точності), ніж метод Ейлера (який маї перший порядок точності).
ПРИКЛАД.
Розв'язати модифікований метод Ейлера рівняння (5.8) з початковою умовою Y(0)=0, на відрізку [0; 4], крок h=1. Результати обчислень заносимо у табл. 5.2.(заповняючи її по строчкам)
Таблиця 2
Рішення рівняння (5.8) модифікованим методом Ейлера
| i | Xi | Yi | Yi’= =f(Xi,Yi) | Xi +1/2 = =Xi+h/2 | Yi+1/2= Yi+h/2*Yi’ | Y’i+1/2= f(Xi +1/2, Yi+1/2) | h* Y’i+1/2 |
| 0.05 | 0.5 | 0.025 | 0.0486 | 0.0486 | |||
| 0.0486 | 0.0473 | 1.5 | 0.0722 | 0.0459 | 0.0459 | ||
| 0.0945 | 0.0446 | 2.5 | 0.117 | 0.0434 | 0.0434 | ||
| 0.138 | 0.0421 | 3.5 | 0.159 | 0.0410 | 0.0410 | ||
| 0.179 |
Дата добавления: 2015-08-26; просмотров: 1060;
