Метод прогонки

При великому n безпосереднї рішення систем (6.5) або (6.7) стаї дуже

нагромадженним. Для рішення систем такого виду було розроблено спеціальний метод, який отримав назву метода прогонки.

Нехай маємо систему (6.5). Розглянемо перше n-1 рівняння

(Y_i+2 - 2Y_i+1 + Y_i) / h² + Pi ( Y_i+1 - Y_i ) / h + gi.Yi=Fi;

(i=1,2,...,n-1)

Переобразовуючи , отримуємо:

Y_i+2+(-2+h.P_i)Y_i+1+(1-h.P_i+h ².g_i)Y_i=h² .F_i (6.10)

Введемо позначення :

M_i=-2+h.P_i; K_i=1-h.P_i+h ².g_i, (i=0,1,2,...,n-2) (6.11)

Тоді (6.10) замінюємо в виді:

Y_i+2+M_i.Y_i+1+K_i.Y_i=h ².F_i (6.12)

Розв'язавши (6.12) відносно Y_i+1, одержимо:

Y_i+1 = h ².F_i / M_i - Y_i+2 / M_i - K _i.Y_i / M_i (6.13)

Нетяжко впевнитися в тому, що, вийнявши Y_i із (6.13) з допомогою крайових умов системи (6.5) , одержимо це рівняння в виді:

Y_i+1=C_i(D_i-Y_i+2) (i=0,1,2,...,n-2) (6.14)

де Ci,di- деякі коефіціїнти.

Нехай, наприклад, i=0; тоді (6.13) прийме вид:

Y₁ = h ².F₁ / M₀ - Y₂ / M₀ - K ₀.Y₀ / M₀ (6.15)

Із крайової умови A0.Y₀+A1 (Y₁ - Y₀) / h =A найдемо Y₀:

Y₀ = A.h /(A₀ - h) - A₁ .Y₁ /(A₀ h - A₁ )

і підставимо його в (6.15). Після преобразовувань одержимо :

Y₁ = 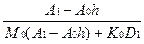[( 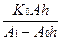+ h² .F₀ ) - Y₂]

Позначимо:

C₀ = 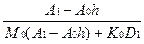; D₀ = 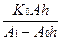+ h² .F₀ (6.16)

Із (6.14) можна записати:

Y_i=C_i-1(D_i-1-Y_i+1)

Підставляючи цей вираз в (6.12), одержимо :

Y_i+2+M_i.Y_i+1+K_i.C_i-1(D_i-1-Y_i+1)=h² .F_i

Звідкіля:

Y_i+1= [(h² .F_i-K_i.C_i-1.D_i-1)-Y_i+2] / (M_i-K_i.C_i-1) (6.17)

Зрівнюючи (6.14) і (6.17), одержимо для знаходження Ci і Di рекурентні формули:

Ci=1 / (M_i-K_i.C_i-1) ; D_i = h² .F_i-K_i.C_i-1.D_i-1 (6.18)

де i=1,2,...,n-2; Ci, Di- прогоночні коефіціїнти.

Метод прогонки полягає з двох етапів: прямого і зворотнього ходу.

На першому етапі (прямий хід) на основі (6.16) знаходжуються коефіціїнти

C₀ і D₀. Після цього, послідовно використовуючи рекурентні формули (6.18)

одержують значення C_i і D_i (i=1,2,...,n-2).

Другий етап (зворотний хід) починається з знаходження Y_n . Використовуючи другу крайову умову (6.5) і формулу (6.14) при і=п-2, запишимо систему

двох рівнянь:

B₀ Y_n + B₁ (Yn -Y_n-1 ) = B;

(6.19)

Y_n-1 = C_n-2 (D_n-2 - Y_n )

Розв'язавши цю систему відносно Yn, одержимо:

Y_n-1 = (B₁.C_n-2.D_n-2 + B.h) / [B₁(1 + C_n-2) + B_O.h] (6.20)

Підставивши в (6.20) уже знайдені прямим ходом С_п-2,D_n-2,знаходимо Y_n.

Після цього обчислюють Y^n-1,Y_n-2,Y_n-3,...,Y₁,послідовно використовуючи рекурентну формулу (6.14):

Y_n-1 = C_n-2(D_n-2 - Y_n);

Y_n-2 = C_n-3(D_n-3 - Y_n-1);

. . . . . . . . . . . . . . (6.21)

Y₁ = C₀(D₀ - Y₂) ;

Значення Y₀ знаходимо по формулі,яка була одержана з першої крайової

умови (6.5) :

Y₀ = (A₁.Y₁ - A.h) / (A₁ - A₀.h) (6.22)

6.4. Алгоритм рішення крайової задачі методом прогонки

1. Обирається h і знаходяться узлові точки X_i;

2. В узлових точках знаходяться коефіціїнти М_і,К_і і F_i (при необхідності);

3. Знаходяться по (6.16) прогоночні коефіціїнти в початковій точці С_о і D_o;

4. По (6.18) розраховуються прогоночні коефіціїнти C_i i D_i ;

5. По (6.20) знаходиться значення Y_n ;

6. Використовуючи формули (6.21) або (6.14) послідовно обчислюють значення

Y_n-1,Y_n-2,..,Y₁.

7. Значення Yo знаходиться по (6.22).

8. Для перевірки точності рішення величина кроку змінюється вдвічі і алгоритм повторюється, починаючи з п.1;

9. Оцінюється точність знайденого рішення способом зрівняння значень Yi i

Yi.Якщо знайдена похибка задовольняє заданій точності,то рішення завершу-

ється.Інакшке обчислювання повторюються з іще зменьшеним вдвічи кроком.