Метод Ейлера
Хай дається рівнення (5.3), задовольняючє початковоі умові (5.4). Рішенням цього рівнення виявляється функція Y=Y(X), яка визначена на інтервалі [a,b]. Для інтегрування скористуємося (5.5), обмежавшись двома членами ряда:
Yi+1 = Yi+h.Yi' = Yi+h.f(Xi,Yi) (5.6)
Інтегрування за методом Ейлера міститься у послідовному застосуванні формули (5.6) до рівнення (5.3), починаючи з k=1. У присутньості початкової умови (5.4) для обчислення Y1 не потрібна додаткова інформація - достатньо обчислити праву частину (5.3) при заданих значеннях Xo та Yo.
Обчислення Y1 аналогічне проведенню дотичної в точці (Xo,Yo), тангенс кута нахилу якої задаїться правою частиною (3) при X=Xo, Y=Yo, до перети-нання з вертикальною прямою, проведенною із точки X=X1 (мал. 5.1). При наступньому кроці, тобто при обчисленні Y2, знов визнача’ться похідна, але вже у точці з координатами (X1, Y1). З цієї точки проводиться дотична до перетинання з прямою X=X2. Аналогічно повторюються обчислення для Y3, Y4,... .
При достатньо малой величини кроку h метод Ейлера дає рішення з достатньою точністью, тому що хиба рішення близька до h2 (h<<1) на кожному кроці інтегрування. До недоліків методу необхідно віднести сильну залежність одержаного рішення від величини кроку h та збільшення об'єму обчислень для досягнення задовільної точністі.
ПРИКЛАД.
Рівнення швидкості послідовно протікаючих реакцій 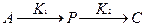
записується у слідуючому вигляді:
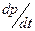 = K1*[Ao]*exp(-K1*t)-K2*[p] (5.7)
= K1*[Ao]*exp(-K1*t)-K2*[p] (5.7)
де [p]-концентрація речовини р на час t від початку реакції; К1=0.05 і К2=0.0065 - константи швидкостей першої та другої реакцій,відповідно,л/(моль*хв); [Ao] - початкова концентрація речовини А.
Знайти,чому будуть дорівнювати значення [p] через 1, 2, 3, 4 хв після початку реакції,
якщо при t=0 [p]=0, a [Ao]=1.
РІШЕННЯ: Позначим Y=[p], X=t.Тоді рівняння (5.7) після підстановки чиселних значень констант прийме вигляд:
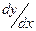 = f(X,Y)=0.05*exp(-0.05*X)-0.0065*Y (5.8)
= f(X,Y)=0.05*exp(-0.05*X)-0.0065*Y (5.8)
Результати обчислень заносимо у табл. 5.1.(заповняючи її по строчкам).Згідно з умовою
задачі крок h=1
Таблиця 5.1
Рішення рівняння (5.8) методом Ейлерa
| i | Xi | Yi | f(Xi, Yi) | h*f(Xi, Yi) |
| 0.05 | 0.05 | |||
| 0.05 | 0.0473 | 0.0473 | ||
| 0.0973 | 0.0446 | 0.0446 | ||
| 0.0143 | 0.0421 | 0.0421 | ||
| 0.184 |
Вирішення задачі - сукупність значень Y(i=0,1,..,4).
Дата добавления: 2015-08-26; просмотров: 605;
