Доказательство. Проверим аксиомы кольца.

Проверим аксиомы кольца.

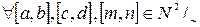
1) 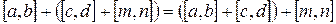(ассоциативность +) (?)

.

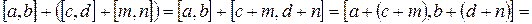
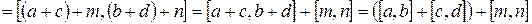2) 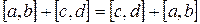(коммутативность +) (?)

.

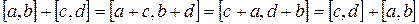3) 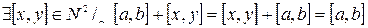(существование 0) (?)

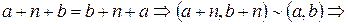
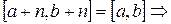
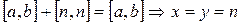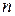, где - произвольное натуральное число.

4) 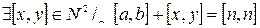(существование противоположного) (?)

.

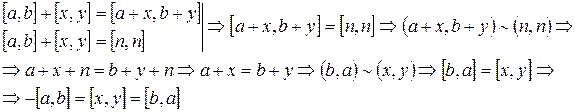5) 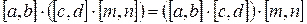(ассоциативность ) (?)

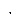6) 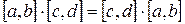(коммутативность ) (?)

.

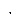7) 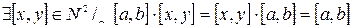(существование 1) (?)

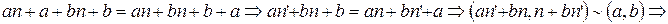
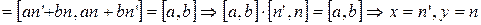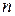, где - произвольное натуральное число.

8) 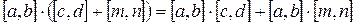(дистрибутивность) (?)

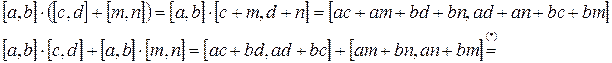
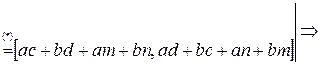
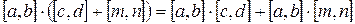
9) 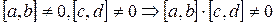(отсутствие делителей 0) (?)

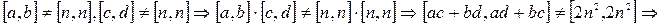
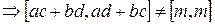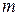, где - произвольное натуральное число, в силу произвольности 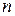. Таким образом, .

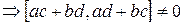что и требовалось доказать.