Вложение полукольца натуральных чисел в кольцо целых.
Договоримся обозначать множество целых чисел через  .
.
Теорема 4. Полукольцо натуральных чисел изоморфно вкладывается в кольцо целых чисел.
Доказательство.
Рассмотрим множество 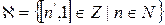 . Покажем, что
. Покажем, что  подалгебра алгебры
подалгебра алгебры  .
.
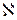 замкнуто относительно сложения и умножения (?)
замкнуто относительно сложения и умножения (?)
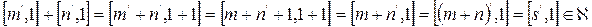
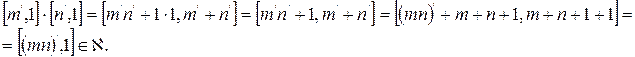
Рассмотрим соответствие 
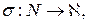 заданное по правилу
заданное по правилу 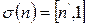
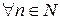 .
.
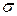 - отображение (?)
- отображение (?)
Всюду определенность очевидна, поскольку для каждого натурального числа 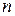 можно построить класс
можно построить класс 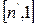 .
.
Однозначность: 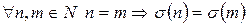 (?)
(?)
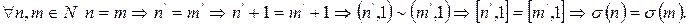 ъ
ъ
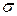 - биекция (?)
- биекция (?)
Инъективность: 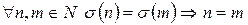 (?)
(?)
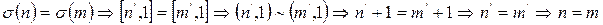 .
.
Сюръективность: 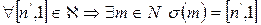 (?)
(?)
Возьмем 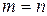 , поскольку
, поскольку 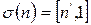 . В силу произвольности
. В силу произвольности 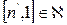 сюръективность доказана.
сюръективность доказана.
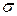 - гомоморфизм (?)
- гомоморфизм (?)
Сохранение операции сложения: 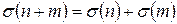 (?)
(?)
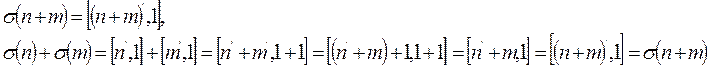
Сохранение операции умножения: 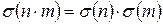 (?)
(?)

Таким образом доказано, что алгебра 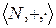 изоморфна подалгебре
изоморфна подалгебре  алгебры
алгебры 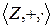 , следовательно,
, следовательно, 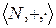 изоморфно вкладывается в
изоморфно вкладывается в 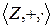 .
.
что и требовалось доказать.
Замечание. Поскольку полукольцо натуральных чисел вкладываются в кольцо целых чисел, то отождествим элементы 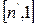 и
и 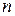 , т.е. будем считать их (тождественно) равными. Ввиду этого отождествления получим
, т.е. будем считать их (тождественно) равными. Ввиду этого отождествления получим 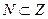 .
.
Дата добавления: 2015-08-21; просмотров: 1048;
