Положительный конус и его свойства.
Определение. К≠{0} называется упорядоченным кольцом, если существует непустое подмножество Р≠ 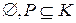 элементов кольца, называемое положительным конусом, удовлетворяющим условиям (аксиомам положительного конуса):
элементов кольца, называемое положительным конусом, удовлетворяющим условиям (аксиомам положительного конуса):
(1) 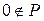 ;
;
(2) 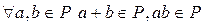 ;
;
(3) 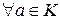
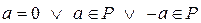 .
.
Теорема 7. Если К – упорядоченное кольцо с положительным конусом Р, то бинарное отношение <, определенное на К по правилу 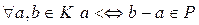 , является строгим линейным порядком.
, является строгим линейным порядком.
Доказательство.
Отношение 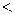 - антирефлексивно (?)
- антирефлексивно (?)
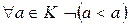 (?)
(?)
Предположим, что 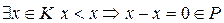 , что противоречит аксиоме (1) положительного конуса, следовательно, предположение неверно.
, что противоречит аксиоме (1) положительного конуса, следовательно, предположение неверно.
Отношение 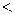 - антисимметрично (?)
- антисимметрично (?)
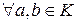 a<b
a<b 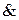 b<a
b<a 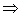 b=a (?)
b=a (?)
a<b 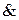 b<a
b<a 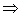 b–a,a–b
b–a,a–b 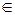 P
P 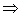
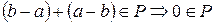 , что противоречит аксиоме (1) положительного конуса. Таким образом, посылка импликации всегда ложна, следовательно, импликация истинна.
, что противоречит аксиоме (1) положительного конуса. Таким образом, посылка импликации всегда ложна, следовательно, импликация истинна.
Отношение 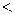 - транзитивно (?)
- транзитивно (?)
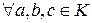 a<b
a<b 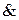 b<с
b<с 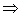 a<с (?)
a<с (?)
a<b 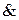 b<с
b<с 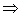 b–a,с–b
b–a,с–b 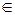 P
P 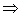
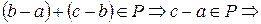 a<c.
a<c.
Отношение 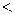 - линейно (?)
- линейно (?)
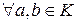 a<b
a<b 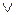 b<a
b<a 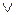 a=b (?)
a=b (?)
Пусть a, b 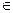 K , b – a
K , b – a 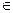 K. По аксиоме (3) положительного конуса возможен один из трех случаев:
K. По аксиоме (3) положительного конуса возможен один из трех случаев:
1. b – a =0, a=b,
2. b – a 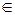 P, a<b,
P, a<b,
3. -(b – a)=a – b 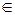 P, b<a.
P, b<a.
что и требовалось доказать.
Свойства отношения 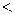 :
:
 выполняется:
выполняется:
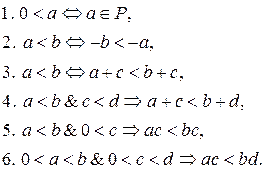
Дата добавления: 2015-08-21; просмотров: 729;
