Доказательство. Проведем методом от противного
Проведем методом от противного. Предположим, что 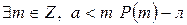 . Рассмотрим множество
. Рассмотрим множество 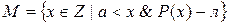 .
. 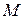 ограничено снизу числом
ограничено снизу числом 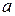 .
. 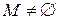 , т.к.
, т.к. 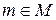 . Тогда, по теореме 13,
. Тогда, по теореме 13, 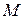 имеет наименьший элемент
имеет наименьший элемент 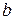 . Покажем, что
. Покажем, что 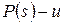 , где
, где 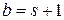 . Предположим, что
. Предположим, что 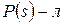 , причем
, причем 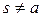 (так как иначе
(так как иначе 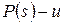 ). Тогда
). Тогда 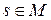 , но это противоречит тому, что
, но это противоречит тому, что 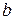 - наименьший в
- наименьший в 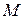 . Согласно индуктивному предположению
. Согласно индуктивному предположению 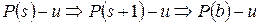 . Последнее противоречит условию
. Последнее противоречит условию 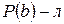 . Значит, предположение неверно, и
. Значит, предположение неверно, и 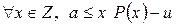 .
.
что и требовалось доказать.
Теорема 11 (ІІ форма): Если утверждение 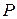 о целых числах верно целого числа
о целых числах верно целого числа 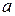 и для произвольного целого числа
и для произвольного целого числа 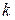 , большего
, большего 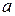 , из верности утверждения
, из верности утверждения 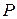 для всех целых чисел
для всех целых чисел  таких, что
таких, что 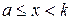 , следует верность утверждения для числа
, следует верность утверждения для числа 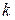 , то утверждение верно для каждого целого числа, большего или равного
, то утверждение верно для каждого целого числа, большего или равного 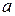 .
.
 .
.
Дата добавления: 2015-08-21; просмотров: 703;
