Типы динамического поведения биологических систем

Биологические системы и математические модели, их описывающие, могут демонстрировать различные типы поведения.

Триггерные системы

Одной из важных особенностей биологических систем – переключение из одного режима функционирования в другой. Модель (система уравнений), описывающая подобное явление, будет иметь два или более устойчивых стационарных состояния, между которыми возможен переход. Такая система называется триггерной.

Пример1.6. В соответствии с гипотезой В.Вольтерра, обобщающей представления о функционировании экологических сообществ, модель конкуренции популяций двух видов задается системой дифференциальных уравнений:

(1.4*)

Здесь переменные 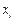– численности видов, параметры – константы собственной скорости роста видов, – константы самоограничений численности (внутривидовой конкуренции), 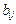– константы взаимодействия видов ( 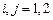). Значения всех параметров в системе (1.4*) положительны.

Пусть , , , , , 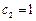. Проведите полный анализ данной системы уравнений.

Решение:

1) Поиск стационарных состояний.

Решаем систему алгебраических уравнений:

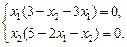
Получаем координаты четырех стационарных состояний:

I) ;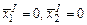

II) – это стационарное состояние соответствует вымиранию вида и достижению видом 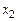стационарной численности 5;

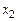III) – аналогично, это стационарное состояние соответствует вымиранию вида и достижению видом стационарной численности 3;

IV) .

2) Построение главных изоклин.

Уравнения изоклин горизонтальных касательных: и 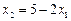. Уравнения изоклин вертикальных касательных: и 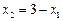. Каждое из уравнений задает прямую. Попарные пересечения изоклин горизонтальных и вертикальных касательных дают стационарные состояния (рис. 1.3).

Рис. 1.3. Главные изоклины системы уравнений, описывающих конкуренцию двух видов (пример 2.1). Сплошные линии – изоклины вертикальных касательных, штрихованные – изоклины горизонтальных касательных

3) Линеаризация системы в окрестности стационарного состояния.

, ,

, .

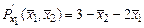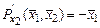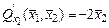В окрестности стационарного состояния 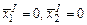матрица коэффициентов линеаризованной системы имеет вид: . Корни соответствующего характеристического уравнения есть . Корни действительные положительные. Таким образом, стационарное состояние 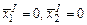является неустойчивым узлом.

В окрестности стационарного состояния матрица коэффициентов линеаризованной системы имеет вид:

. Корни соответствующего характеристического уравнения есть Оба корня действительны и отрицательны. Второе стационарное состояние является устойчивым узлом.

В окрестности стационарного состояния матрица коэффициентов линеаризованной системы имеет вид:

. Корни соответствующего характеристического уравнения есть Аналогично случаю II оба корня действительны и отрицательны. В этом случае третье стационарное состояние является устойчивым узлом.

В окрестности стационарного состояния матрица коэффициентов линеаризованной системы имеет вид:

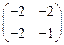. Корни соответствующего характеристического уравнения есть В четвертом стационарном состоянии имеем седловую неустойчивость.

Строим фазовый портрет (рис.1.4).

Рис. 1.4. Фазовый портрет системы уравнений, описывающих конкуренцию двух видов (пример 1.6.)

Получили триггер: два устойчивых и один неустойчивый узел разделены седлом. В зависимости от начальных условий в системе реализуется одно из двух возможных устойчивых стационарных состояний. Результат можно интерпретировать как выживание одного из двух конкурирующих видов.

Колебательные системы

Для биологических систем характерно периодическое изменение различных характеристик. С некоторыми из типов периодических изменений мы уже имели дело при рассмотрении особых точек типа центр, фокус. Однако часто в живых системах наблюдаются колебания, обладающие особым отличительным свойством: неизменностью во времени периода и амплитуды колебаний,означающей стационарность и устойчивость колебательного режима. В данном случае периодическое изменение величин представляет собой один из типов стационарного поведения системы. Если колебания имеют постоянный период и амплитуду, устанавливаются независимо от начальных условий и поддерживаются свойствами самой системы, без воздействия периодической силы, система называется автоколебательной. В фазовом пространстве такому типу поведения соответствует предельный цикл – притягивающее множество. Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости.

Предельные циклы могут быть устойчивыми и неустойчивыми. Предельный цикл устойчив, если существует такая область на фазовой плоскости, содержащая этот предельный цикл – окрестность , – что все фазовые траектории, начинающиеся в окрестности , асмиптотически при 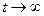приближаются к предельному циклу. Внутри устойчивого предельного цикла обязательно есть неустойчивая точка типа фокус или узел. Необходимым условием рождения устойчивого предельного цикла является переход (бифуркация) типа стационарного состояния от устойчивого фокуса к неустойчивому (действительная часть соответствующих характеристических чисел 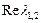через 0 переходит от отрицательных значений к положительным, при этом мнимая часть характеристических чисел 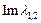отрицательна). После такой бифуркации возможность существования устойчивого предельного цикла сохраняется до тех пор, пока значение 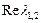остается положительным.

Пример: Брюсселятор – базовая модель, является классическим примером автоколебательного поведения переменных (концентраций) в системе химических реакций. Брюсселятор представляет собой следующую схему гипотетических реакций:

, , , .

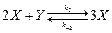Здесь А, В – исходные вещества, C, R – продукты, X, Y – промежуточные вещества. Пусть конечные продукты C и R немедленно удаляются из реакционного пространства. Это означает, что обратные константы 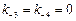. Если субстрат A находится в избытке, то . Предполагают также, что 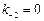. Значения остальных констант приравнивают 1. Тогда рассматриваемая схема реакций описывается системой уравнений:

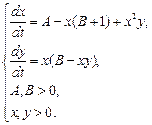
Определите тип стационарных значений на всей плоскости допустимых значений параметров. Укажите область значений параметров, в которой возможно существование предельного цикла.

Решение:

1. Найдём стационарные состояния системы:

→ → →

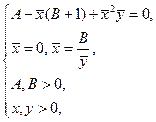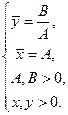
2. Исследуем тип стационарной точки и ее устойчивость.

Найдем коэффициенты линеаризации:

1) Определим знак для ответа на вопрос об устойчивости:

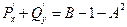
При 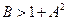выполнено неравенство 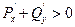, значит, в этой области параметров стационарная точка неустойчива.

При выполняется неравенство 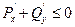, таким образом, в этой области параметров стационарная точка устойчива.

2) — седел не существует.

3) фокус или узел? надо определить знак подкоренного выражения в формуле для вычисления характеристических чисел :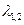

.

Это выражение отрицательно при выполнении неравенства 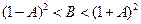. Таким образом, при 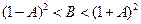в системе должны наблюдаться колебания.

При и 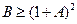колебаний в системе не будет.

При 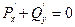происходит смена устойчивости стационарного состояния типа фокус, в этот момент происходит рождение предельного цикла.

Получившиеся результаты можно представить в виде параметрической диаграммы (рис.1.5).

Рис. 1.5. Параметрическая диаграмма